|
5.5 Variance
The term variance was used to describe the square of the standard deviation R.A. Fisher in 1913. The concept of variance is of great importance in advanced work where it is possible to split the total into several parts, each attributable to one of the factors causing variations in their original series. Variance is defined as follows:
Variance = 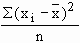
Standard Deviation (s. d.)
It is the square root of the arithmetic mean of
the square deviations of various values from their arithmetic mean.
it is denoted by s.d. or s.
Thus, s.d. ( sx
) = 
= 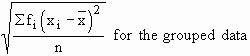
where n = S
fi
Merits : (1) It is rigidly defined
and based on all observations.
(2) It is amenable to further algebraic treatment.
(3) It is not affected by sampling fluctuations.
(4) It is less erratic.
Demerits : (1) It is difficult to
understand and calculate.
(2) It gives greater weight to extreme values.
Note that variance V(x) =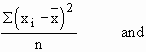
and s. d. ( sx ) =
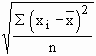 and
and 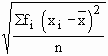
Then V ( x ) = 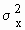
[next page]
|