The world of numbers : We can represent the number system in the form of a rough sketch as follows.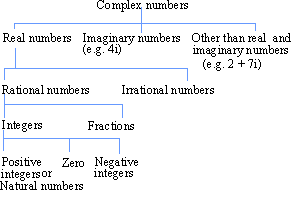

Natural numbers : The numbers 1, 2, 3, ......are called natural or counting numbers i.e. N = {1, 2, 3, ......}

Whole numbers : The numbers 0, 1, 2, 3, ----- are called whole numbers i.e. W = {0, 1, 2, 3, ........}

Integers : The numbers ........-3, -2, -1, 0, 1, 2, 3, ------ are called integers i.e. I = {.....-3, -2, -1, 0, 1, 2, 3, ......}

(i) The numbers .......-3, -2, -1 are called Negative integers.

(ii) The numbers 1, 2, 3, ..... are called Positive integers.

Rational numbers : p and q (q ¹ 0) are integers. The number where , then is known as a rational number. Thus the set Q of the rational numbers is given by Q =

Naturally, fractions such as are called rational numbers. This definition also emphasizes that any integer can also be a rational number since p = p / 1, p Î I.

Terminating and repeating decimals are also rational numbers, since they can also be put in form p/q.

Odd numbers : Whole numbers which are not divisible by 2 are odd numbers. For e.g. 1, 3, 5, 7, 9.......

Even numbers : The numbers which are divisible by 2 are even numbers. For e.g. 0, 2, 4, 6, 8, ...... are even numbers.

Prime numbers : This is a number that can be divisible by 1 and itself only i.e. it has exactly two factors i.e. 1 and itself. Euclid has shown that there are infinite number of prime numbers. The integers 2, 3,5, 7, 11, 13 etc. are prime numbers.

Composite numbers : Any integer having more than one prime factor i.e. the numbers divisible by more than just 1 and itself, is called a composite number. All composite numbers can be expressed as products of unique set of prime numbers. This fact is also referred to as the fundamental theorem of arithmetic or the unique factorization theorem. For e.g. 4, 6, 8, 9, 10..... are composite numbers.

Let us recall some notations which are used for certain specific sets. We list them below as :

N : The set of all natural numbers (i.e. positive integers). This is the set. {1, 2, 3, ....., n, ......}

I : The set of all integers i.e. {......, -3, -2, -1, 0, 1, 2, 3.....}

W : The set of all whole numbers i.e. {0, 1, 2, 3, ......}

Q : The set of rational numbers.

R : The set of real numbers.

C : The set of all complex numbers.

[next page]

Index

Introduction
1.1 Pre-requisties
1.2 Common Mathematical Symbols
1.3 Some Properties of Basic Mathematical Operations
1.4 Real Numbers

Chapter 2