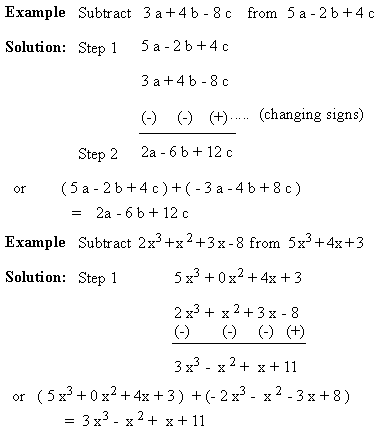An algebraic expression which consists of two or more terms is called a polynomial.
For example, a + b, x³ - y³ , x² + x y + y².

1) A polynomial which consists of exactly two terms is a binomial.
For example 2 x² + x, x² + y².

2) A polynomial which consists of exactly three terms is a trinomial.
For example, x² + 3 x + 2, a² + a b + b² etc. Usually a polynomial is written either in the ascending or descending powers of the variable, say x. This form of a polynomial is called a standard form. For example x⁴ + 3 x³ + x² + 7x + 5 and 2 + 3 y + 7 y² - y³ are polynomials in the standard form. Descending order is used more commonly.

In order to add given polynomials, we adopt two steps.

1) Arrange the given polynomials, such that like terms are in one column.

2) Add the coefficients of each column separately.

Subtraction :

This is done in two steps :

1) Arrange the given polynomials, such that like terms are in one column.

2) Change the signs of the terms of the polynomial and then add.

[next page]

Index

3.1 - Introduction
3.2 - Monomial, Polynomials
3.3 - H.C.F and L.C.M

Chapter 4