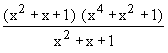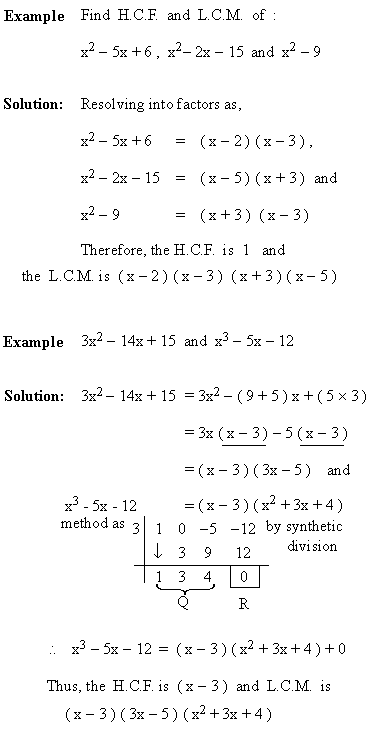
Example x2 - 1 ; x2 + 3x + 2 ; x2 + 4x + 3 Solution: x2 - 1 = ( x - 1 ) ( x + 1 ) x2 + 3x + 2 = ( x + 2 ) ( x + 1 ) x2 + 4x + 3 = ( x + 3 ) ( x + 1 ) \ H.C.F = ( x + 1 ) and L.C.M = ( x - 1 ) ( x + 1 ) ( x + 2 ) ( x + 3 )
H.C.F. and L.C.M. by long division method. If the factors of a given polynomial cannot be found out easily and degrees are not same, then we may employ another method known as long division method for finding out H.C.F. and L.C.M. 1) Take higher degree polynomial and divide it by the other polynomial of lower degree till we get zero remainder. Then the divisor is the H.C.F. ( G.C.D.) of the two polynomials. L.C.M. =Example Find G.C.D. and L.C.M. of x2 + x + 1 and x4 + x2 + 1 Soltuion: Dividing the higher degree polynomial x4 + x2 + 1 by the lower degree polynomial x2 + x + 1 as : 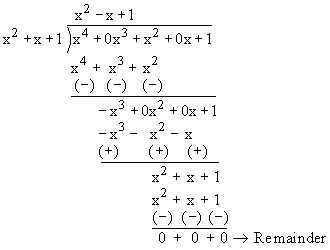
Therefore, G.C.D.= x2 + x + 1 and L.C.M. = = x4 + x2 + 1 2) If the remainder is not zero, then divide the divisor by remainder till the latest remainder is zero. Then the second divisor ( i.e. the first remainder ) is G.C.D. If > again remainder is not zero, continue the process till you get remainder zero. The last divisor is the G.C.D. and L.C.M. = 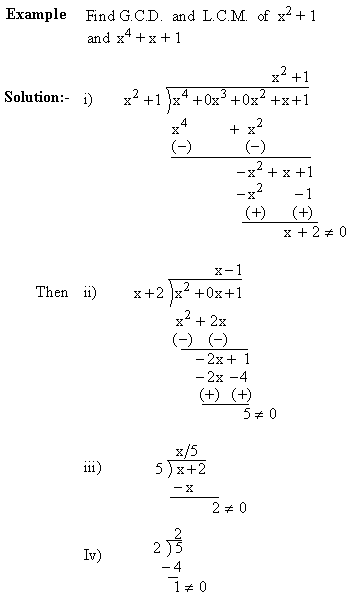
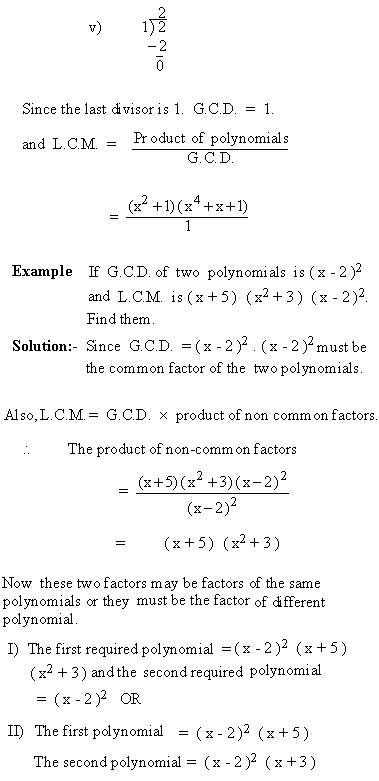
********** |
3.1 -
Introduction Follow @Pinkmonkey_com  |