Special relations : A and B are two non-empty sets. If each element of set the A is associated with exactly one element of set B, then this association is called a function from set A to set B.

Note :-

1. Set A is the domain

2. Set B is the co-domain

3. All the elements of set B need not have association

4. The element of set B which are associated is the set "range" of the function. Thus the range is a sub-set of co-domain.

   For example, { ( 2, 9 ) , ( 3, 13 ) } is a function
   { ( 2, 5 ), ( 3, 9 ) } is not a function

5. The element y Î B such that the function say 'f ' associates to the element x Î A is denoted by f ( x ) i.e. y = f ( x ) and y is called the 'f ' image of x or value of 'f ' at x. The element x is also called pre-image of y. Every element of A has a unique image but each element of B need not have an image of an element in A. There can be more than one element of A which has the same image in B.

6. We denote the range of f : A ® B by f (A) Thus f ( A ) = { f ( x ) | x Î A } Þ f ( A ) Î B.

7. The domain variable is often referred as the independent variable and the range variable is referred to as the dependent variable.

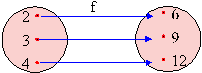
1. An arrow diagram can be used.

   For example if f : x ® 3 x, x Î { 2, 3, 4 } then f can be shown as