|
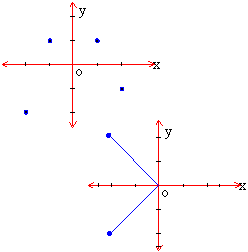
Determination of Domain, Range and if the relation is a function Example A relation is given as { ( 1, 1 ), ( 2, 1/2 ), ( 3, 1/3 ), ( 4, 1/4 ) } is it a function ? Justify. If yes, then state its domain and range. Exhibit the relation by a formula. Solution : Let A = { 1, 2, 3, 4 } and B = { 1, 1/2 , 1/3, 1/4 }. Every element in A occurs once and only once in the ordered pairs and related to one and only one element of set B, exhibiting a relation. Hence it is a function from set A to set B. Let it be 'f ' then, Domain of 'f ' = set A = { 1, 2, 3, 4 }Range of 'f ' = set B = { 1, 1/2 , 1/3, 1/4 } Also the second member of each ordered pair is the reciprocal of its first member. If we denote member of A as x and that of B by y then, y = 1/x Þ f ( x ) = 1/x x Î A Example Observe the following graphs. Determine whether the relations are functions or not. If so, state their domain and range. Solution : Function : Yes (1) Domain = { -2, -1, 1, 2 } Range = { -2, 1, 1, -1 } Domain = { x | -2 £ x £ 0 } (2)
Range = { y | -2.5 £ y £ 2.5 } No, it is not a function. Example If f ( x ) =Solution : Since 'f ' is a real valued function 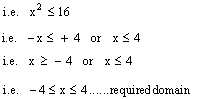
|
Index
6.1 Relations 6.2 Functions 6.3 Variation Chapter 7 |