Example Graph the solution set of each of the following :
i) 2 x - y > 2 ii) x 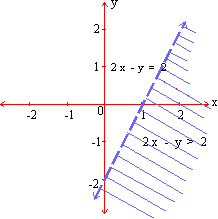- 2 y £ 4 iii) 2 x + y £ 0

Solution:
i) Consider the line 2 x - y = 2 It meets x- axis at (1,0) and y- axis at (0, -2). The boundary is drawn passing through (0, 0). When we put x = 0 and y = 0 then the inequality, we get 0 - 0 > 2 i. e. 0 > 2. Thus the origin determined by the inequality is the half-plane which is the non-origin side of the boundary line. Further it is a strict inequality (>) therefore, the solution set is the open-half plane as shown in the figure.

ii) The bounding line is x-2 y = 4 which meets x- and y- axis at points (4, 0) and (0, -2) respectively. The coordinates x = 0 and y = 0, satisfy the inequality x - 2 y < 4 . Therefore, the graph of the solution set is the closed half-plane containing the origin as shown in the figure.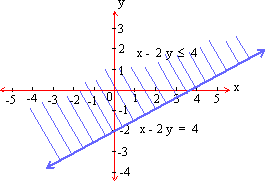

iii) The boundary line 2 x + y = 0 passes through (0, 0) and its slope is negative. If we put x = 1, y = 0 in 2 x + y £ 0 we get 2 £ 0. Hence (1,0) does not satisfy the inequality. Hence the graph of the solution set is the closed half -plane which does not contain the point (1,0) as shown in the figure.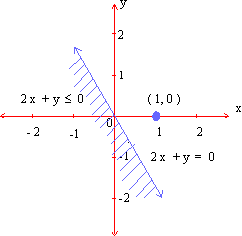

* * * * * * * * * *

Index

7.1 Definition
7.2 Simultaneous Equations
7.3 Inequations (Inequalities)
7.4 Absolute Values

Chapter 8