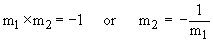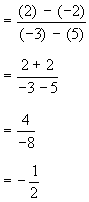Between the graph of a linear equation and the equation itself, one can have two types of relationships I) The slope of the straight line II) Its intercepts.

Slope: In mathematics the word 'slope' has a specific meaning (see figure). Thus slope of segment MN is the ratio of the difference between y - coordinates of point M and N to the corresponding difference between their x - coordinates respectively.

Slope of segment MN =

Where x₁ ¹ x₂ means that the x - coordinates of both M and N should be different. But if x₁ = x₂ then the segment is parallel to y - axis i.e. it is a vertical segment which has no slope. Slope of any non-vertical segment can be always found. Slope of any line is the slope of any segment of it.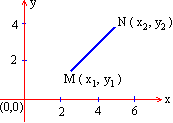

Note that :

1. Slopes of parallel lines are equal.

2. The slopes of a line parallel to the x - axis and the x - axis itself is zero. (Horizontal lines).

3. The slope of a line parallel to the y - axis and the y - axis itself has no slope or this slope is undefined. (vertical lines).

4. A line having a positive slope makes an acute angle with the positive direction of the x - axis.

5. A line having a negative slope, makes an obtuse angle with the positive direction of the x - axis.

6. The products of slopes of two mutually perpendicular lines is always -1 i.e. if two mutually perpendicular lines have slopes m₁ and m₂ respectively then

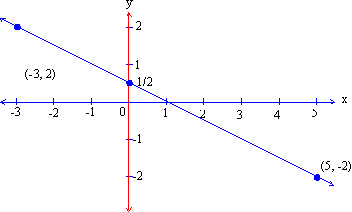
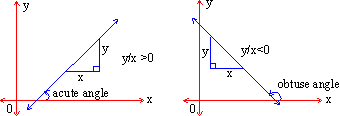Example Find slope 'm' of the straight line through (-3, 2) and (5, -2)

Solution : (x₁, y₁) = (-3, 2) and (x₂,y₂) = (5,-2)

Therefore slope (m) =

Index

8.1 Definition
8.2 Relations, Graphs and Symmetry
8.3 Slopes and Intercepts

Chapter 9