|
2.2 Inequalities
| x | = a means x = - a or x = + a
| x | < a means - a < x < a
| x - a | = d means x = a - d or x = a + d
| x - a | £ d means a - d £ x £ a + d
0 < | x - a | < d means a - d < x < a + d Except x = a
0 < | x - a | £ d means a - d £ x £ a + d Except x = a
Examples
-
| x - 3 | < 1
\ 3 - 1 <
x < 3 + 1 i.e.
2 < x <
4
| x - 2 | < 0.01
\2 - 0.01 < x < 2 + 0.01 i.e. 1.99 < x < 2.01
0 < | x - 1 | < 0.01
\ 1 - 0.01 < x < 1 + 0.01 except x = 1
i.e.0.99 < x < 1.01 except x = 1
0 < | x - 5 | £ 0.01
\ 4.99 £ x £ 5.01 except x = 5
d - neighborhood of a ( d - nbd of a )
If the open interval ( a - d, a + d ) for the variable x ( say)
It means a - d < x < a + d
It means | x - a | < d
It means x lies in the open interval ( a - d, a + d )
I means x belongs to d - nbd of a
It means d is closed to a by less than d
Note that all these statements mean the same thing | x - a | <
d
Example 1 Write down the 0.01 nbd of 3 in the interval form
Solution : d - nbd of a means ( a-d , a + d )
Here a = 3 and d = 0.01
\ 0.01 nbd of 3 = ( 3-0.01, 3 + 0.01)
= ( 2.99, 3.01 )
Example 2 State any two values of x such that | x -5 |< 0.001
Solution : | x - 5 |< 0.001 i.e. 5 - 0.01 < x < 5 + 0.001
i.e. 4.999 < x < 5.001
Thus any two values of x in ( 4.999 < 5.001 ) are 4.9999 and 5.0001
Example 3 State any two values of x such that x is closer to 1/3 by less than 0.01.
Solution : x is closer to 1/3 by less than 0.01 can be put in the form | x - 1/3 | < 0.01 i.e. x belongs to the interval ( 1/3 - 0.01, 1/3 + 0.01)
Any two values in this interval of x are 0.323 and 0.340
Example 4 Find three values of x, satisfying the inequality | 2x - 1 | < 0.05
Solution : | 2x - 1 | < 0.05
\ 2x belongs to the interval ( 1 - 0.05, 1 + 0.05 )
i.e. ( 0.95, 1.05 )
\x e 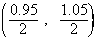 i.e. ( 0.475, 0.525 ) i.e. ( 0.475, 0.525 )
any three values of x are 0.49, 0.50, 0.5001.
|