8.3 Volumes
(I) Volumes of solids with known cross sections
If we know the formula for the region of a cross section, we can find the volume of the solid having this cross section with the help of the definite integral.
(1) If the cross section is perpendicular to the x-axis and itís area is a function of x, say A(x), then the volume (v) of the solid on [ a, b ] is given by v = 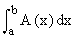
(2) If the cross section is perpendicular to the y-axis and its area is a function of y, say A(y), then the volume (v) of the solid on [ a, b ] is given by v =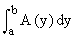
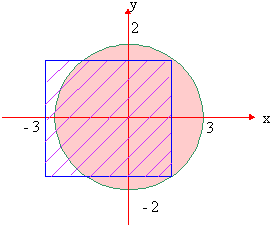
Example 13 Consider a solid whose base is the region inside the circle x2 + y2 = 4. If cross sections taken perpendicular to the x-axis are squares. Find the volume of this solid.
Solution : Let A be the area of an arbitrary square cross section which is perpendicular to the x-axis
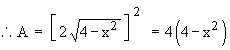
Therefore the volume of the solid 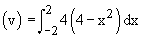
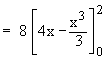

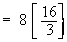
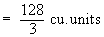
Example 14 A solid has its base is the region bounded by the lines x + 2y = 6, x = 0 and y = 0 and the cross sections taken perpendicular to x-axis are circles. Find the volume the solid.
Solution : The cross section is a circle, perpendicular to the x-axis. Naturally the diameter of this circular cross section has its ends on the x-axis and the line x + 2y = 6, which the function of x.
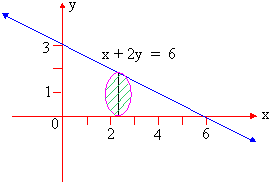
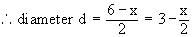
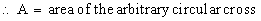
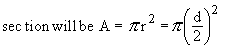
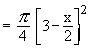
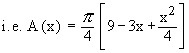
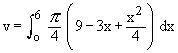
\ The volume (v) of the solid is
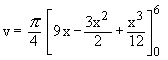
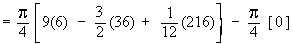
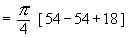
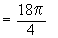
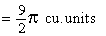
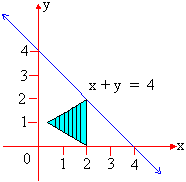
Example 15 A solid has its base is the region bounded by the lines x + y = 4, x = 0 and y = 0 and the cross section is perpendicular to the x-axis are equilateral triangles. Find its volume.
Solution : The cross section is an equilateral triangle, perpendicular to the x-axis. Its side has its ends on the line x + y = 4 and the x-axis.
\ Side (s) = 4 - x
[next page]
|