Disk Method :
In this type, the axis of revolution is the boundary of the plane region and its cross sections are taken perpendicular to the axis for revolution. The name 'disk method' is due to the fact that the cross section of a disk is a circle of area pr2, the volume of each disk to the product of its area and its thickness.
(A) If the disk is perpendicular to the x-axis, then its radius would be expressed as the function of x , say f (x).
Thus the volume of a solid generated by revolving the area of the region bounded by y = f (x) and the x- axis on [a, b] about the x- axis is given by
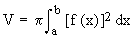
(B) If the disk is perpendicular to the y-axis, then its radius would be expressed as the function of y say, f (y).
Thus the volume of the solid generated by revolving the area of the region bounded by x = f (y) and the y- axis on [c , d] about the y - axis is given by
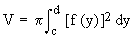
(C) The volume of the solid generated by the revolution about any line (axis) A' B' is given by
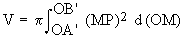
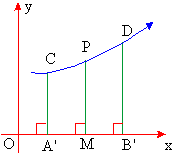
where P is any point on the curve and PM is drawn perpendicular to A' B' .
Example 16 Find the volume of the solid generated by revolving the region bounded by x2 = 8y, the lines y = 0 and y = 1 about the y - axis.
Solution : Here the y-axis is the boundary of the region. Using disk method as,
The volume (V) of the solid is
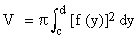 and f (y) = x Ž [f (y)]2 = 8y and f (y) = x Ž [f (y)]2 = 8y
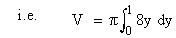
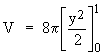
= 4p
[1 - 0]
= 4p
cubic units.
[next page]
|