Example 23 Find the volume of the solid generated by revolving the region bound by y = x2 + 2 and y = x + 8 about the x-axis.
Solution : Solving y = x2 + 2 and y = x + 8, we get
x2 + 2 = x + 8 i.e. x2 - x - 6 = 0
\
(x - 3) (x + 2) = 0
\
x = -2, x = 3
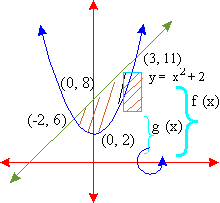
The graph will intersect at points (-2, 6) and (3, 11) (see figure) As the x-axis is not the boundary of the given planar region bounded by the two curves, we use the washer method. Let f (x) = x + 8 and g (x) = x2 + 2 ... f (x) > g (x) and the limits of integration being a = -2 and b = 3
Then the required volume (of revolution) Is
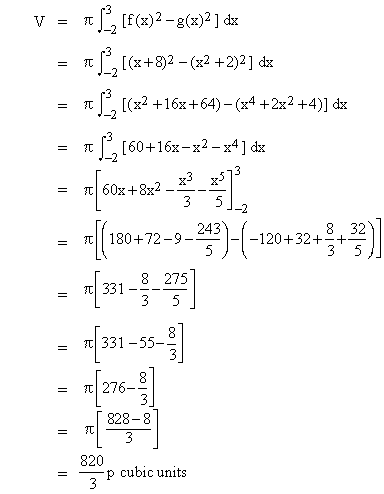
Example 24 Find the volume of the solid generated when the plane region bounded by the curves y = x2 and y = 3 - 2x is revolved about the x-axis.
Solution : y = x2 and y = 3 - 2x
\
x2 = 3 - 2x
\
x2 + 2x - 3 = 0
\
(x + 3) (x - 1) = 0
\
x = -3, x = 1
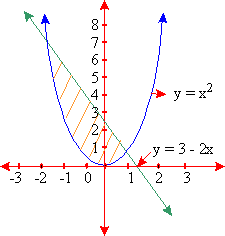
The two curves intersect at points (-3, 9) and (1, 1)
Clearly, x-axis is not the boundary of the region bounded by the two curves. Using the washer method, the volume of the required solid is
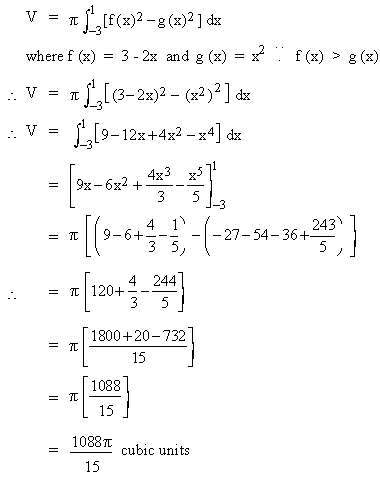
(III) Volume of Revolutions by Shell method
The cylindrical shell method is used to find the volume of solids of revolution, when the cross sections of the solid are taken parallel to the axis of revolution.
Let r be the radius of a shell of height 'h' . Its volume will be (2p
rh ´
thickness). In first term of this product i.e. 2p
rh, 'r' is expressed in terms of x, if the axis of revolution is vertical i.e. the y-axis. The radius 'r' will be expressed in terms of y, if the axis of revolution is y-axis (horizontal axis). Height will be expressed in terms of f (x) or f(y)respectively. Therefore volume (V) of the solid generated by revolving the region bounded by y = f (x) and x-axis on [a, b], f (x) ³
0, about the y-axis is
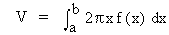
the volume of a solid generated by rotating the region bound by x = f (y) and y - axis on [a, b], f (y) ≥ 0 is given by
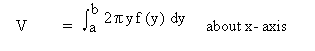
Example 25 Find the volume of the solid, when the region bounded by y = 4, y = x2 is revolved about the line y = -1, using the shell method.
Solution : Expressing r and h in terms of y as
Let (x, y) be any point on the curve y = x2 Then we have, r = y - (-1) = y + 1 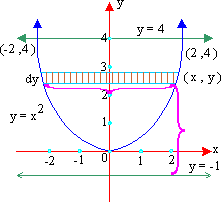
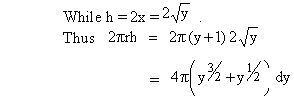
The limits of integration are y = 0 to y = 4
\ The volume of revolution (V) is
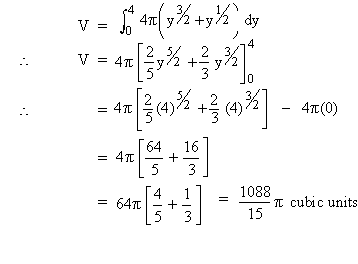
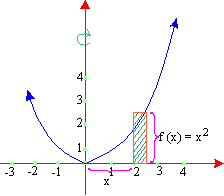
Example 26 Find the volume of the solid generated by revolving the region bounded by y = x2 and the x-axis on [1, 3], about the y-axis.
Solution : Here we will use the cylindrical shell method. Expressing 'r' and h in terms of x as r = x and h = f (x) = x2 (see figure), then the volume (V) of the solid is
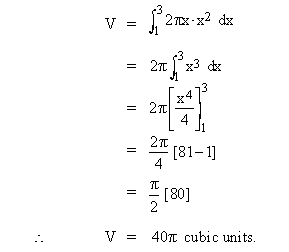 
[next page]
|