|
This equation of exchange, therefore, may be viewed as an identity: the market value of all goods and services must be equal to the supply of money multiplied by the velocity of the circulation of one unit of currency.
Fisher has also presented an extended version of the equation of exchange. For this purpose he had introduced bank money or credit (M1) and its velocity or circulation (V1). The equation of exchange in its full form can then be stated as:
MV + M1V1 = PT
But it can be assumed that MV includes both currency and credit money and hence it can be stated in its simplified form:
MV = PT
(B) Value of money: The equation of exchange is used by classical economists mainly for explaining fluctuations in the value of money. Otherwise in its original form the equation is a truism or an identity. It simply explains total money supply (MV) is equal to total monetary expenditure (PT). While using it for explaining transitions in the value of money two fundamental assumptions are made. These are related to the behavior of 'V' and 'T'. It is assumed that:
i) 'V', the velocity of circulation of the currency depends upon consumption patterns of the people and the size of their income. Both these things are not likely to alter significantly in the short run with any changes in the quantity (M) of money. Therefore over a short interval 'V' can be assumed to be constant.
ii) The trade volume (T) or level of real income (Y) depends upon the availability of resource supplies and technological conditions. These factors are not likely to alter in the short run with the variations in the quantity of money (M). If these two assumptions are granted then the only dependent variable that remains in the equation is the price level 'P'. Hence the conclusion at once follows: with 'V' and 'T' remaining constant, 'P' will vary directly and proportionately with 'M'. This can be illustrated :
Let M = 300, V = 4, T = 600 the P will be equal to 2.
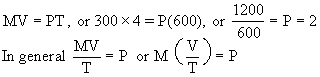
But since 'V' and 'T' are constant 'M' and 'P' must vary directly and proportionately. If M is doubled P will also be doubled.
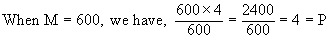
Similarly when 'M' is halved P is also halved,
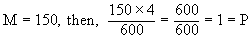
|