|
(G) Consumers’ Surplus: Marshall has analyzed consumers’ surplus as a part of demand behavior. Such a surplus of utility that a consumer enjoys is a result of the law of diminishing marginal utility. While utility that a consumer experiences from every additional unit consumed goes on falling, the market price that he has to pay for all the units is uniform. Hence actual money expenditure (which is objective) and the utility received (which is subjective) do not add up to the same value. The extra utility that a consumer enjoys is called Consumers’ Surplus.
This concept can be described variously. It is the difference in consumer satisfaction arising out of his subjective and objective evaluations. It may also be described as the extra satisfaction that the intra-marginal units bring to a consumer. It can also be explained as the area under the demand curve. This can be illustrated as:
|
No. of units consumed |
MU |
Price |
Consumers’ Surplus
(Mu-P) |
|
1 |
5 |
2 |
3 |
|
2 |
4 |
2 |
2 |
|
3 |
3 |
2 |
1 |
|
4 |
2 |
2 |
0 |
|
5 |
1 |
2 |
- |
|
6 |
0 |
2 |
- |
|
|
|
|
6 (Total CS) |
In the example we have 6 units of a good. The marginal utility that a consumer enjoys from these units, goes on falling as…5, 4, 3, 2, 1 and 0. The market price is $2 per unit. Assuming each of the utility units to be worth a dollar, the consumer will equate Mu with price. Consumer equilibrium occurs at the fourth unit where Mu = Price = 2 which maximizes the consumer’s total satisfaction. For purchasing 4 units of the good he has to spend $8 (an objective evaluation) but he actually receives a total utility of 14 units (5 + 4 + 3 + 2) from the four units he purchases. Thus he receives 6 units of ’extra’ satisfaction (14 - 8 = 6): this is the consumers’ surplus. This arises from the fact that though the consumer equates utility (the marginal units) with the price, the earlier or intra-marginal units are more valuable (a subjective valuation) for him, in terms of utility enjoyed. This has further been explained in Figure 26.
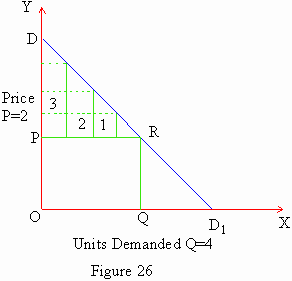
In the figure, DD1 is the demand curve. Units of the good have been shown on the horizontal axis and price is shown on the vertical axis. At price OP (i.e. $2) there is consumer equilibrium. The consumer purchases OQ (4) units. His total expenditure is $8 (4 xð 2) which is equal to the area of the rectangle OPRQ. The total utility that the consumer enjoys from the four units purchased is equal to the area DRQO. The difference between the two areas would be the area of the triangle DRP (DRQO - PRQO = DRP). This is the surplus satisfaction that the consumer enjoys. The numerical value of the consumers’ surplus in our example is 6 units. However, the geometrical measure of the surplus is somewhat larger. It is equal to the area of the triangle DRP (half the base into altitude) = ˝ (PR x PD). PR = OQ = 4 and PD = OD - OP = 6 - 2 = 4. The geometric value of consumers’ surplus is ˝ (4 x 4) = 8 which is larger than 6.
Consumers’ Surplus is considered a somewhat hypothetical or imaginary concept. It has considerable importance in framing practical policies such as those of taxation, foreign trade, welfare promotion etc.
(H) Market Demand Curve: So far we have discussed marginal utility, equilibrium and demand of a single consumer. The actual market as such has numerous consumers. An interesting question arises regarding the construction of such a market demand curve and its behavior.
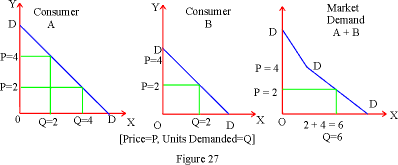
Figure 27 shows the method of construction of a demand curve for the entire market. We have two consumers A and B with two demand curves which have different slopes. Consumer A demands 2 units of a good when price is $4 but he demands 4 units of a good when the price is $2. Consumer B has no demand for the good at price of $4 but he demands 2 units of the good when its price falls to $2. The market demand curve shows the total demand of the two consumers as 2 units at price $4 (2 + 0) and as 6 units (4 + 2 = 6) when price is $2.
Such a geometric addition of demand curves is also known as lateral summation of demand. The market demand curve is flatter or more flexible than the individual demand curve. This is because of the fact that at every price the total demand in the market is much larger than that of any individual.
**********
|