10. Ð B = 2 ÐC                           ( \ Ð C = Ð B )

    and Ð B = 2 Ð A

    Hence Ð A = Ð C = x (say )

    then ÐB = 2 x

    and 2x + x + x = 180 gives x = 45⁰

    i.e. hence Ð A = Ð C = 45⁰ and ÐB = 2 x = 90⁰

    \ side opposite Ð B is the largest and sides opposite Ð A and ÐC are equal.

    Hence AB = BC

    \ AB² = BC²

    \ AB² < BC² + AC²

    Hence B.

11. Two important facts namely

    (a) 0 < x < 1 implies x to be a positive proper fraction and

    (b) x  - :     =
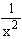
    Since x < 1. \ x² < x. \ x2 < 1 ( \ x > 1 ) and hence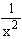 > 1.

    (Since the reciprocal of proper positive fraction is more than 1).

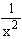    \ > x2

    x ^-2 > x2

    Hence A.

12. Given 0 < a < b < c
    The sum a + b can be small. i.e. 1 + .1 or 1.1 or it can be very large,
    i.e. 1 + 1000 i.e. 1001.
    Similarly c - a can be very small. 1.2 - 1 i.e. .2 or can be very large,
    i.e. 100001 - 1 i.e. 100000.

    Hence D.

    OR Mathematically

    a + b ³ c - a        or     a + b < c - a

    If a + a ³ c - b     or     a + a < c - b

    If 2a ³ or a <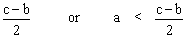

    If c and b are very close then c - b or 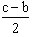can be very small but if c is very large compared to b, c - b or 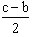can be very large
    a can be more than or less than or even equal to .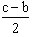

    Hence D.

    [next page]

Index

Test 1

Section 1 : Verbal Section
Section 2 : Quantitative Section
Section 3 : Analytical Section
Section 4 : Quantitative Section
Section 5 : Verbal Section
Section 6 : Analytical Section
Section 7 : Verbal Section
Answer Key To Test 1

Answer Explanation To
Test 1
Section 1 : Verbal Section
Section 2 : Quantitative Section
Section 3 : Analytical Section
Section 4 : Quantitative Section
Section 5 : Verbal Section
Section 6 : Analytical Section
Section 7 : Verbal Section