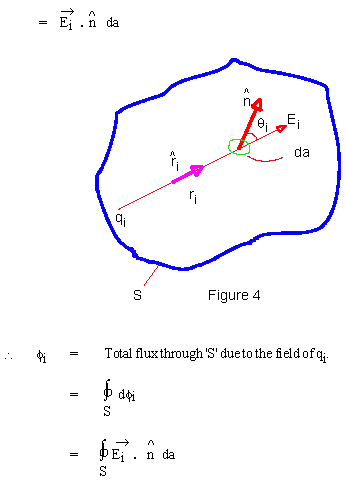
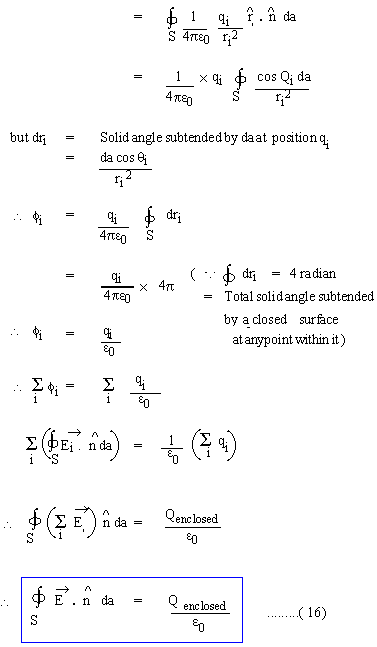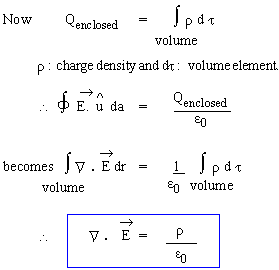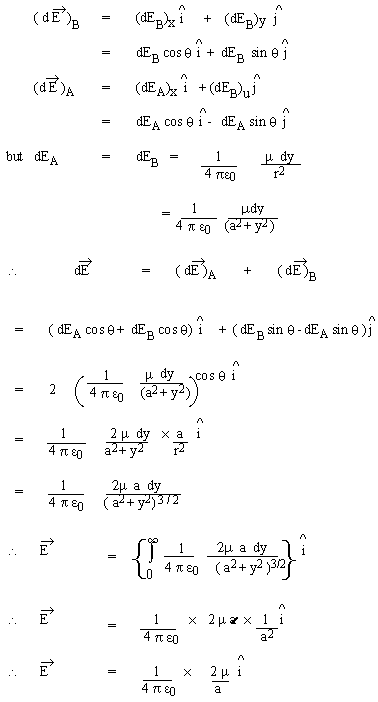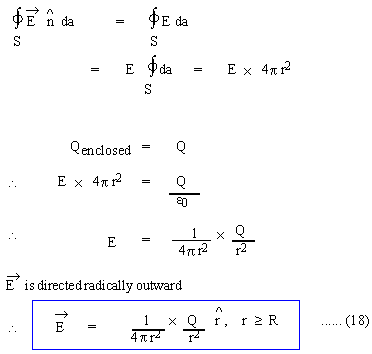19.3 Gauss's law

"The electric flux through a closed surface is equal to the net charge enclosed within the surface divided by the permittivity " is the statement of Gauss's law.

where 'S' is a closed Surface.

'da' is the elementary area on 'S'

is unit outward normal vector to 'S' at the position of 'da'.

Q_enclosed is total net charge enclosed within 'S'.

= flux through 'da' due to field of qi

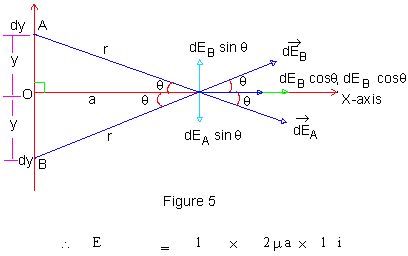
Equation (16) is called an integral form of Gauss's law. Even in this form it has tremendous power to determine E for a system of charges having certain kinds of symmetry, in a simple manner, compared to calculations by super position principle. But, when expressed in differential form, it forms one of the four field equations of Maxwell and thus becomes one of the pillars on which the edifice of Classical Electromagnetic field theory is based.

In Vector analysis, one of the theorem is,

known as Gauss's Divergence theorem.

As an illustration of power in Gauss's law, consider determination of due to infinitely long and uniformly charged conducting wire.

Click here to enlarge

The choice of X - axis is only for convenience; the directions of is radially outwards from the conductor,

The same result can be obtained by using Gauss's law.

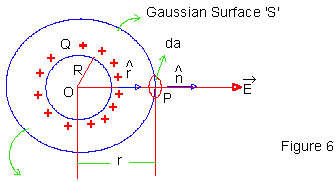
Fields of Spherical charged conductor and infinitely large plane conductor

Spherical charged Conductor

(i) Points outside or on the sphere,

Spherical charged conductor, Radius: R, total charged and surface density of charge

It is obvious that the charge on the sphere behaves as if it is concentrated at the centre, in so far as the field at is concerned.

(ii) Points inside the Sphere, (r < R )

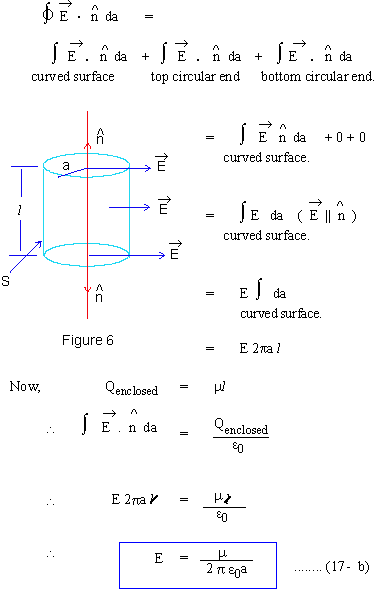
Infinitely large conducting plane

[next page]

Index

Chapter 20