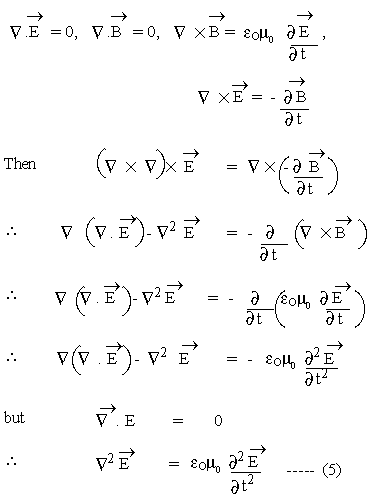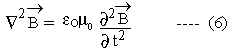CHAPTER 28 : MAXWELL'S FIELD EQUATIONS AND ELECTRO-MAGNETIC WAVES In our discussion earlier, it has been pointed out that the four basic experimental laws on which the science of Electro-magnetism is based, can be represented in the form of differential equations. This was obtained for the first time by Maxwell. These are
For simplicity and for the purpose of illustration the discussion is restricted to Electro magnetic field in Vacuum. If there are no free changes and the free currents are in the vacuum then the above equations become.
Equation (5) is a wave equation, the solution to which, propagates as a wave i.e. E propagates as a
wave in vacuum with velocity Likewise for the field
Thus, Electro-magnetic field propagates in vacuum with the speed of light; and light therefore must be an electro-magnetic wave. ********** |
Chapter 28 : Maxwell's field equations
and electro-magnetic waves Follow @Pinkmonkey_com  |
Gauss's law in Electro-Static is based on Coulomb's law of force between stationary charges
Similar as above in Magnetism, but free mono-poles do not exist.
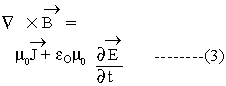Modified Ampere's law for magnetic fields formed due to time-dependent currents.
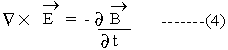Faraday's Law of electro-magnetic induction.
, it is easy to show that
