r = a sec q \ r = 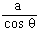
\ r cos q = a
\ x = a which is a straight line parallel to y - axis at a distance 'a' units from the origin.
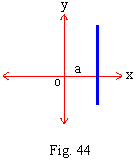
r = a (1 + cos q) = r = a + a cos q
\ r. r = ar + ar cos q or r2 - ar cos q = ar
then (r2 - ar cos q)2 = a2r2
\ [x2 + y2 - ax]2 = a2 [x2 + y2]
This is a cardioid.
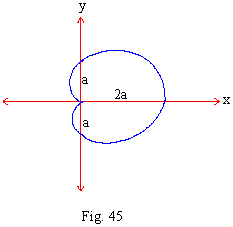
r = a (1 + sin q ) \ r = a + a sin q
\ r . r = a.r + a r sin q
\ r2 - ar sin q = ar
\ (r2- ar sin q)2 = a2 r2
\ [x2 + y2 - ay]2 = a2 [x2 + y2 ] which is cordioid
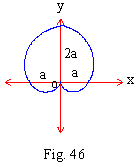
r = 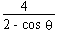
\ 2r - r cos q = 4
\ 2r = 4 + r cos q
\ (2r)2 = ( 4 + r cos q)2 \ 4r2 = ( 4 + r cos q )2
\ 4 ( x2 + y2 ) = ( 4 + x )2 or
3x2 + 4y2 - 8x -16 = 0
which is the rectangular form of an ellipse.