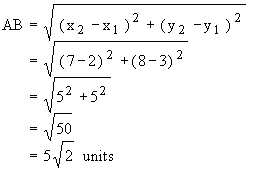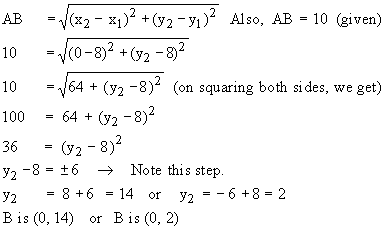1) A relation is a set of ordered pairs of numbers. Relations are usually written in the set builder notation.

For example {(x, y) | y £ x}, { (x, y) | y = x² + 1 } etc.

In most cases we just write y £ x, y = x² + 1 etc.

Many a times we just give the list of ordered pairs { (1,2) , (3,5), (-2,6) }

A relation can be best understood by sketching its graph.

First, we will study graphic equations on the coordinate plane.

To graph an equation on the co-ordinate plane, find the solutions by giving a value to one variable and this will help solve the other variable. Then graph the solutions.

Example Find the distance of the point A(3,4) from 0 [origin].

Solution : A (x₁, y₁) = ( 3, 4 )

Distance of A from the origin 0, is

Example Find the distance between the points (2,3) and (7,8)

Solution : Let A (x₁, y1) = (2, 3) and B (x₂ , y₂) = (7, 8)

Distance between points A and B, is.

Example The distance between the point A (8,8) and a point B on the y - axis is 10. Find the Coordinates of B.

Solution : Since point B is on the y-axis, B is (0, y₂)

Let A (x₁, y₁) = (8, 8)

The distance between A and B, is

Index

8.1 Definition
8.2 Relations, Graphs and Symmetry
8.3 Slopes and Intercepts

Chapter 9