|
CHAPTER 1 : FUNCTIONS
1.1 Functions And Mapping
Definition: Let A and B be any two non-empty
sets. Let A = {p, q, r} and B = {a, b, c, d}. Suppose by some rule
or other, we assign to each element of A a ‘unique’ element of B.
Let p be associated to a, q be associated to b, r be associated
to c etc. The set {(p, a), (q, b), (r, c) } is called a function
from set A to set B. If we denote this set by ‘f’ then we write
f : A ® B which is read as "f " is
a function of A to B or ‘f’ is a mapping from A to B.
Definition: Let A and B be two non-empty
sets. Suppose there exists a rule of correspondence, denoted by
f which associates to each member of A, a unique member of B. Then
‘f’ is called a function or a mapping from set A to set B.
It is denoted by f : A ® B or A 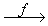 B B
Note that :
-
The set A is called "domain" of 'f '
The set B is called "codomain" of 'f '
The element y Î B which the function 'f' associates to the element x Î A is denoted by f(x) i.e.
y = f(x) and y is called the 'f ' image of x or value of ' f ' at x. The element x is also called as pre-image of y. Every element of A has a unique image but each element of B need not have as the image of an element in A. There can be more than one element of A which has the same image in B.
The set of these images in B is called the range of ' f ' i.e. the range of a function as the images of its domain. We denote the range of f : A ® B by f (A). Thus f (A) = { f (x) : x Î A } Þ f (A) Í B.
If A and B are any two non-empty sets, then a function f from A to B is a subset f of A ´ B satisfying the following conditions:
(i) 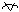 x Î A, (x ,y) Î f for some y Î B x Î A, (x ,y) Î f for some y Î B
(ii) (x , y) Î f and (x, y1)
Î f Þ
y = y1
The first condition ensures that there is a rule which assigns to each element x Î A some element y Î B. Thus each element in A will have an image. The second condition guarantees that the image is unique.
In other words, a function is a set of ordered pair (x, y), such that for each first element x, there corresponds a unique element y.
-
The domain variable is often referred as the independent variable and the range variable is referred as the dependent variable.
|
Index
Introduction
1.1 Functions And Mapping
1.2 Functions, Their Graphs and Classification
1.3 Rules for Drawing the Graph of a Curve
1.4 Classification of Functions
1.5 Standard Forms for the equation of a straight line
1.6 Circular Function and Trigonometry
Chapter 2
|