|
2.6 Evaluating Limits
Limits of functions are evaluated by using many different methods ( techniques ) such as recognizing a type, simple substitution, factorization, simplification, rationalization etc. Let us solve a few examples by using each of these methods.
1. Substitution
Example 1 Evaluate lim ( 5x2
- 7x + 9 )
x®3
Solution : Let L = lim ( 5x2-
7x + 9 )
x®3
= 5 (3)2 - 7 (3) + 9 \ x ¹ 3
= 33
i.e. when x is replaced by 3, (5x2 - 7x + 9 ) ® 33
Hence lim ( 5x2 - 7x + 9 ) = 33
x® 3
2. Factorization
Example 2 Evaluate 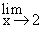 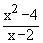
Solution : Let L = 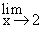 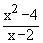
Direct substitution of x = 2 yields 0/0 form which means less. By Factoring, simplifying and then substituting we find that
L = 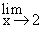 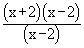 = = 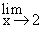 ( x + 2 ) ( x + 2 )
= 2 + 2 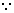 x ¹ 2 x ¹ 2
= 4
Note that the graph of y = 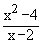 is the same as the graph
of y = ( x + 2 ) except it has a break at (2,4) is the same as the graph
of y = ( x + 2 ) except it has a break at (2,4)
Example 3 Evaluate 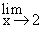
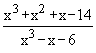
Solution : Let L = 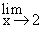 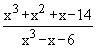
Substituting x = 2 yields 0/0 form which is meaning less. Hence ( x - 2 ) must be a factor of both numerator and denominator. Let us factorize them by synthetic
division.
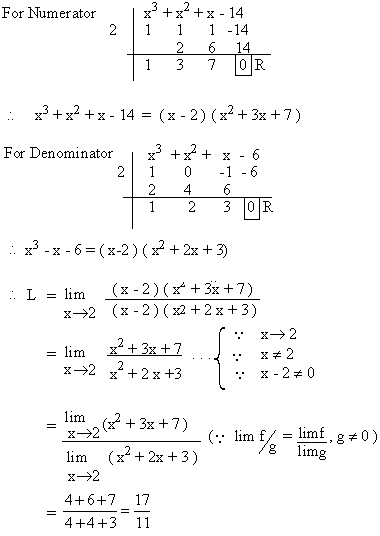
|