|
3.3 Some Very-often-encountered Continuous Functions
1) A constant function is one that is continuous everywhere
Let f (x) = k, k being a constant
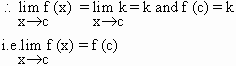
Therefore ’f ’ is continuous at x = c. As ’c’ is
any real number. ’f’ is continuous everywhere.
2) The ’Identity’ function is continuous
everywhere.
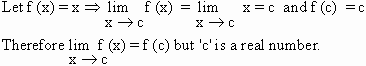
Thus the identity function is continuous everywhere.
3) The Polynomial functions are continuous everywhere.
Let f(x) = P0 + P1x + P2x2 + ..........Pnxn, n Înon-negative integer with P0 , P1 , P2, ......Pn are real constants. Then f (x) is called a polynomial of degree ’n’
Since P0 , P1 , P2, ......Pn are real constant Þ They are continuous every where.
Also, x, x2,...xn are continuous everywhere.
Using the fact that (f +g) and (fg) are continuous and
if f and g are continuous functions of x every where we can say
that the polynomial function f(x) is also continuous every where.
4) Rational function is continuous.
Let f (x) = 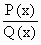 where P(x) and Q(x) are polynomials in x having no common factors, then f (x) is called a rational function.
The f (x) is defined for all real x except those
x for which Q(x) = 0 Using the fact if ’f’ and 'g' are continuous,
then f/g is also continuous, f(x) =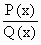
is continuous for all x, except x for which Q(x) = 0.
5) Modulus function is continuous every where.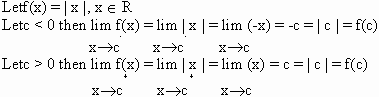
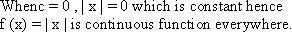
6) sinx, cos x, tan x, csc x, sec x, cot x, arc sin x, arc cos x, arc tan x, arc tan x, arc csc x, arc sec x and arc cot x, ex, ax (a > 0), logax (a > 0, x ¹ 1)are all continuous in their respective domains of definition.
[next page]
|
