4.2 Arithmetic Mean
This is the most commonly used average which you have also studied and used in lower grades. Here are two definitions given by two great masters of statistics.
Horace Sacrist : Arithmetic mean is the
amount secured by dividing the sum of values of the items in a series
by their number.
W.I. King : The arithmetic average may be
defined as the sum of aggregate of a series of items divided by
their number.
Thus, the students should add all observations (values of all items) together and divide this sum by the number of observations (or items).
Ungrouped Data
Suppose, we have 'n' observations (or measures) x1 , x2 , x3, ......., xn then the Arithmetic mean is obviously 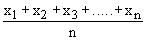
We shall use the symbol x (pronounced as x bar) to denote the Arithmetic mean. Since we have to write the sum of observations very frequently, we use the usual symbol ' S ' (pronounced as sigma) to denote the sum. The symbol xi will be used to denote, in general the 'i' th observation. Then the sum, x1 + x2 + x3 + .......+ xn will be represented by 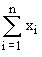 or or 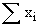 simply simply
Therefore the Arithmetic mean of the set x1 + x2 + x3 + .......+ xn is given by,
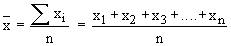
This method is known as the ''Direct Method".
Example A variable takes the values as given
below. Calculate the arithmetic mean of 110, 117, 129, 195, 95,
100, 100, 175, 250 and 750.
Solution: Arithmetic mean = 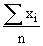
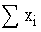 =
110 + 117 + 129 +195 + 95 +100 +100 +175 +250 + 750 = 2021 =
110 + 117 + 129 +195 + 95 +100 +100 +175 +250 + 750 = 2021
and n = 10
Indirect Method (Assumed Mean Method)

A = Assumed Mean = 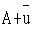
Calculations:
Let A = 175 then
Sui = -65, -58, -46, +20, -80, -75,-75, +0, + 75, +575
= 670 - 399
= 271/10 = 27.1
\
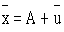
= 175 + 27.1
= 202.1
|