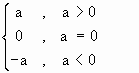Division : The quotient of a real number a by b (b ¹
0) is defined by ab-1 and is denoted by or
a / b or The numbers (a - b) and Axioms of order in R : For a, b, c as real numbers : 1. One and only one of the following must hold a > b , a = b or a < b .... (Trichotomy axiom) 2. If a < b and b < c then a < c....(Transitive axiom) 3. If a < b then a + c < b + c .....(Addition property) or a > b then a + c > b + c 4. Let a < b then (i) for c > 0 then ac < bc .....(Multiplication property) (ii) for c < 0 then bc < ac Some More Results : 1. If a > 0 and b > 0 then ab > 0 2. If a > b and c > d then a + c > b + d but a - c > b - d 3. If a > b then - a < - b i.e. when multiplied or divided by a negative number, the sign of the inequality reverses. 4. If a > b > 0 and c > d > 0 then ac > bd 5. If a < b < c then 0 < b - a and c - b < c - a 6. If 0 < a < b then 7. If a, b Î R then ab
£
Absolute value or Modulus of a Real number The absolute value of any number ‘a’ is denoted by |a| 1. Definition : |a|, a R is defined ’a’ if a is positive or zero, and - a if ’a’ is negative i.e. |a| = e.g. |2| = 2 since a = 2 > 0 |0| = 0 since a = 0 and | - 2 | = - (- 2) = 2 since a = -2 < 0 We assume that all the rational as well as the irrational numbers have been represented on the line 'l' and there is no point left on the line 'l' which does not represent a number. Real numbers : Rational and irrational numbers taken together form the set of real numbers, denoted by R. Clearly N Í I Í Q Í R. The number line is called 'Real number line' as every real number is represented uniquely by a point on this line and conversely each point on the real number line represents a real number. Thus there is one-one correspondence between real numbers and the points on the real number line. 3. Definition: The absolute value |a | of a Î R is defined to be equal toÖ a2 . Thus Ö a2 = |a | 
|
Introduction
Follow @Pinkmonkey_com  |
or 
or
a ¸ b or by ab-1 itself .
are uniquely defined.
i.e. on reciprocating the sign of the inequality reverses.
