Show the following sets with the help of Venn diagrams.

1. A is a set of first four alphabets.

2. B = { x | x is an even number and x < 10 }

3. C = { c | c Î N and 3 < c < 10 }

1) A = { a, b, c, d }

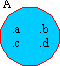
2) B = { 2, 4, 6, 8 }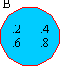

3) C = { 4, 5, 6, 7, 8, 9 }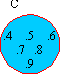

Now if B is a part of A i.e. B contains at least one element less than A then B is called the proper subset of A and show by B Ì A. But if A and B have exactly the same elements i.e. A = B then B is called the improper subset of A and it is written as B Í A or A Í B

1. Thus every set is a subset of itself .
2. Every set has an empty set as its subset.

For example

1) A = { 1, 2, 3, 4, 5, 6, 7 } and B = { 1, 4, 5, 7 }
    Then B Ì A

2) B = { x | x2 -3x + 2 = 0 } and E = { 1, 2 }
    Then E Í B or B Í E Þ B = E

Universal set : Suppose A, B and C are given sets. Then any set of which A, B and C are subsets is called the universal set.

Note that an universal set is the main set or a set of totality of elements of all sets under consideration under a particular discussion. In the universal set once fixed cannot be changed during that discussion. Thus the universal set cannot be unique but changes from problem to problem. The universal set is usually denoted by È or X.

Index

2.1 Sets
2.2 Operations on Sets
2.3 The Algebra of Sets

Chapter 3