6 is a factor of 6, 12 12 is a factor of 12 Domain:- It is the set of all elements which are the first component of the set of ordered pairs and represent a particular relation. For example:- If R = { ( 1, 1 ), ( 1, 2), ( 2, 1 ), (2, 2 ) } then the domain is { 1, 2 } Range:- It is a set of all the second components of the ordered pair and represent a relation. For example :- R = { ( a, c ), ( a, d ), ( b, c ), ( b, d ) } then range = {c, d } Properties of relations
For example R = { ( 1, 1 ), ( 2, 2 ), ( 3, 3 ), In symbols 1) ( x, y ) Î R Þ ( y, x ) Î R D ABC ~ D PQR Þ D PQR Þ D ABC ~ = similar to i.e. x R y and y R z Þ x R z For example, 8 is greater than 6 and 6 is greater 4, then 8 is greater than 4. i.e. 8 > 6, 6 > 4 Þ 8 > 4. If a relation is reflexive, symmetric and transitive then it is an Equivalence relation. |
Index
6.1 Relations 6.2 Functions 6.3 Variation Chapter 7 |

 3
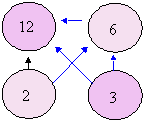
is a factor of 3, 6, 12
3
is a factor of 3, 6, 12