| Linear Inequalities and Half - planes :
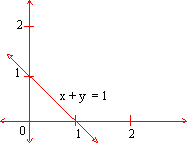 Consider the equality ( or equation) x + y = 1 . . . (1) involving two variables x and y. The solution set of this equality is the set of all ordered pairs (x, y) of the values of x and y , that satisfy the equation ( 1 ). When we graph the solution set, we obtain a straight line. Now let us consider the single inequality x + y £ 1 . . . (2) The solution set of this inequality consists of all ordered pairs (x, y) of the values x and y satisfying x + y = 1 or x + y < 1 . 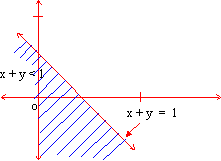 When we graph the solution set of the inequality (ii) , we obtain the points on the line x + y = 1 and the points outside this line (see fig. ) The line x + y = 1 divides the plane into two parts and it is called the ’ bounding line ’ and the two parts are called as the two half-planes. It is clear that the solution set of the inequality is the set of all points on one side of the two of the boundary line i. e any one of the two half-planes. The exact half-plane is determined by testing any point on the boundary line. If its co-ordinates satisfy the inequality, then the side (half - plane) containing that point is represented by the inequality, otherwise the opposite is represented by the inequality. Generally the origin (0, 0) is used if the boundary line does not pass through (0, 0) . The side in which (0, 0) lies is the origin side. The other side obviously is the non-origin side of the boundary line. Now in x + y < 1 if we put x = 0 and y = 0 then the inequality is satisfied. Hence the solution set of x + y < 1 is the set of all points in the plane which are on the origin side of the origin. Thus the solution set of the inequality (ii) contains all points of the line (i) and all the points which are on the origin side of the line (i) as shown in the figure 2. The set of points determined by a linear inequality in x and y is called half - plane. A half - plane is said to be closed or open depending on whether the bounding line is included (£ or ³) or not included ( < or > sign) . For example, the half plane represented by x + y ³ is the closed half plane on the non - origin side, because it includes the line x + y = 1. x + y > 1 is the open half-plane on the non-orgin side of the bounding line. This half - plane does not contain the line x + y = 1. The bounding line is shown by a dashed line on the graph To summarize what has been discussed, we have an inequality or an inequation in two variables and x and y is an expression of the type: a x + b y £ c (or < c) . . . (1) a x + b y ³ c (or > c) . . . (2) where a, b, & c are real numbers. The graph of an inequality is drawn in the following steps:
If the half-plane is closed (i. e. inequality is £ or ³ ) then a thick bounding line is drawn and if the half-plane is open (i. e. inequality is < or > ) then a dashed bounding line is drawn.
|
7.1 Definition |
