|
1.4 Classification Of Functions
Analytically represented functions are either Elementary or Non-elementary.
The basic elementary functions are :
1) Power function :
y = xm , m ÎR
2) Exponential function :
y = ax , a > 0 but a
¹ 1
3) Logarithmic function :
y = log ax , a > 0,
a ¹ 1 and x >
0
4) Trigonometric functions :
y = sin x, y = cos x, y = tan x,
y = csc x, y = sec x and y = cot x
5) Inverse trigonometric functions
y = sin-1
x, y = cos-1x, y = tan-1x,
OR y = cot-1x, y = cosec-1x,
y = sec-1x.
y = arc sin x, y = arc cos x, y = arc tan x
y
= arc cot x, y = arc csc x and y = arc sec x
Note that an elementary function is a function which may be represented by a single formula like y = f (x) where f(x) is made up of basic elementary functions and constants by means of a finite number of operations of addition, subtraction, multiplication, division and taking the function of a function (composite function).
Consider the following examples :
-
y = 1, 2, 3 ........ n [ y = f (n) ] is not elementary as the number of operations that must be performed to get y is not finite but it increases with 'n'.
-
A function 'f ' is defined as
f (x) = x2 if 0 £ x £ 1
= 3x + 1 if 1 £ x £ 2
It is not elementary as it is not represented by a single formula but two formulae.
Single valued function : For each value of x, suppose there corresponds one and only one value of y, then y is called a singled valued function.
e.g. 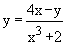 , , 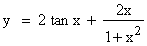 , y = 2 logx + 4e2x , y = 2 logx + 4e2x
|