|
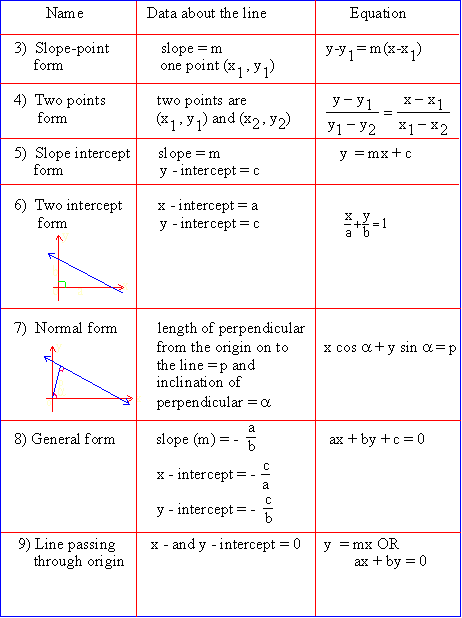
1.5 Standard Forms For The Equation Of A Straight Line
-
A vertical line has equation x = a ( y-axis has equation
x = 0 ) , a Î R
A horizontal line has equation y = b (x-axis has equation y = 0), b Î R
 Click here to enlarge
Click here to enlarge
If two straight lines are a1x +
b1y + c1 = 0 and a2 x + b2y
+ c2 = 0
then 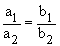 ¹ ¹ 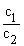 for parallel lines for parallel lines
and (a1a2 + b1b2
= 0 ) for mutually perpendicular lines.
Example 1 If f : R ®
R. f(x) = 4x-3 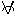 x
Î R. Find f -1, also
find f o f -1 and f -1 o f. x
Î R. Find f -1, also
find f o f -1 and f -1 o f.
Solution :
f : R ® R is one-one onto. Hence f -1
exists and f (x) = 4x - 3
Let y = f ( x ) = 4x-3 then 4x = y+3 \ x = 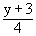
\ f -1
: R ® R is given by f -1
( y ) = 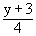
or f -1 R ®
R is given by f -1 (x) = 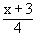 (replacing y by x)
(replacing y by x)
\ (f -1
o f ) : R ® R is given by
( f -1 o f ) ( x ) = f -1
[ f(x) ] = f -1 ( 4x-3 ) = 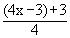 = x
= x
and (f -1 o f) : R ®
R is given by
( f o f -1 ) ( x ) = f [ f -1 (x) ] = 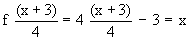
Example 2
Let f : R ® R and g : R ®
R and f (x) = x3 and g (x) = x2 + 1.
Find (1) f o f (2) g o g (3) g o f (4) f o g
Solution :
(1) ( f o f ) : R ® R is given as :
( f o f ) ( x ) = f [ f (x) ] = f [x3]
= (x3) 3 = x9
|