|
(2) ( g o g ) : R ® R is given as :
( g o g ) ( x ) = g [ g (x) ] = g [ x2 + 1 ] = (x2+1)2 + 1 = x4 + 2x2 + 2
(3) ( g o f ) : R ® R is given as :
( g o f ) ( x ) = g [ f (x) ] = g [ x3] = (x3) 2 + 1 = x6 + 1
(4) ( f o g ) : R ® R is given as :
( f o g ) ( x ) = f [ g (x) ] = f [ x2 + 1 ] = (x2+1)3
Example 3
If f(x) = log x and f (x) = x3
, show that
f [ f (2) ] = 3 f (2)
Solution :
L. H. S.
f [ f (x) ] = f [ x3 ] = log ( x3 ) = 3 log x
Put x = 2 then f [ f (2) ] = 3 log 2
R. H. S.
f ( x ) = log x Þ f ( 2 ) = log 2
\ 3 f (2) = 3 log 2
\ L.H.S. = R.H.S.
Example 4
If f (x) = x7 - 5x5 + 3 sin x show
that
f (x) + f (-x) = 0
Solution :
f (x) = x7 - 5x5 + 3 sin x is an odd function
\ f (-x) = -f (x) = - [ x7 - 5x5
+ 3 sin x ]
\ f (x) + f (-x) = 0
Example 5
If f (x) = ( Öx )x show
that 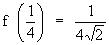
Solution :
f (x) = ( Öx ) x Þ 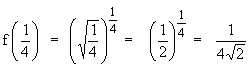
|