|
Example 5 Prove that 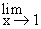
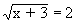
Solution : f(x) = 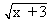 , l = 2 and a = 1. , l = 2 and a = 1.
Given e > 0 we must find d > 0
such that | 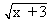 - 2 | < e , 0 < | x - 1 | < d ---------- (1) - 2 | < e , 0 < | x - 1 | < d ---------- (1)
Multiplying the left side by 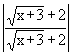 we see we see
That 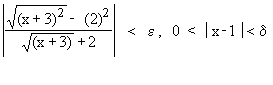
or 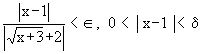 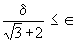 ------ (2) ------ (2)
If we agree to take d < 1, then | x - 1 | < d Þ x Î ( 0, 2 )
and hence 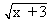 + 2 > Ö3 + 2. Thus, if | x - 1 | < d < 1 then + 2 > Ö3 + 2. Thus, if | x - 1 | < d < 1 then
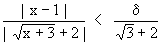
If we pick d = min ( 1,
Î (Ö3 + 2 )) then 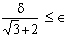
hence (2) holds. Thus 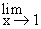 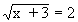
Note :"One-sided" limits always exist for
an important class of functions - namely, monotone functions
Note : From our previous discussion and
problems, we can consider the following four possible behaviors
of functions x ® a.
(1) f(x) may tend to a finite limit , say l
(2) f(x) may tend a
(3) f(x) may tend -a
(4) f(x) may neither tend to l nor ¹ a
In the above possibilities (2) and (3) comes under "infinite limits." Some functions
approaches in the positive or negative direction (i.e. increasing or decreasing without
bound) closer to certain values for an independent variable. When this takes place, the
function is said to have an infinite limit; you write
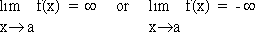
Then the function has a vertical 'asymptotes' at x = a. If either of the above limits holds true.
Limit of a function ' f ' as x ®
¥
Here we suggest the following four possible behaviours of a function 'f' as x® ¥.
(1) f(x) may tend to finite limit l
(2) f(x) may tend ¥
(3) f(x) may tend -¥
(4) f(x) may neither tend to a finite limit l nor ¹
¥
|