|
Example 9 Find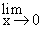 
cot x
Solution : As x®
0 the function cot x has an infinite limit. i.e.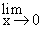
cot x = ± ¥.
To stress the fact that the function cot x can assume as x®0, both positive values ( for x > 0 ) and negative values ( for x < 0 ), we write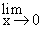
cot x = ± ¥.
Example 10 Find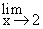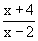  
Solution : The limit of the divisor i.e.
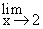(x - 2) = 0 and the limit of the dividend, i.e.
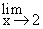(x + 4) = 2 + 4 = 6. Taking the notation 
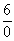in the indicated meaning, we obtain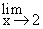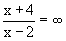 
Example 11 Find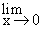 
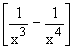
Solution :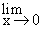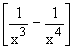 
Rewriting  ,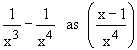
the numerator tends to -1 and the denominator tends
to 0 through positive values of x ( x > 0 ) from
the right. Thus the function decreases without bound and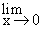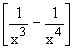 
The function has a vertical asymptote at x = 0.
Example 12 Evaluate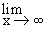  
Solution : In such examples we
use the result
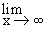
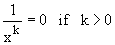
Also, for finding limit of a ratio of two polynomials in x, as x® ¥, we divide all terms of the ratio by the highest degree of the two polynomials. A similar procedure is also possible in many cases for fractions containing irrational terms.
\ Let L =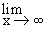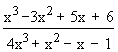
= 
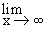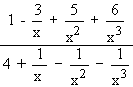
...... Dividing by x3 we get
Taking limits as x ® ¥, i.e.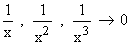 
L =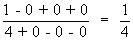 
|
