| CHAPTER 6 : INTEGRATION
We know that in algebra the operations of addition and subtraction, multiplication and division form reverse pairs of operations. In calculus the operations of derivative and integration (anti-derivative) are also thought of an inverse of one another. Thus they also form a reverse pair of operations and the rules for finding derivatives will be useful in establishing corresponding rules for finding anti-derivatives.
6.1 Anti - Derivatives ( Indefinite Integrals )
If a function f exists , for a given function f, such that f˘ ( x ) = f ( x ), then f is called anti-derivative of f.
An anti-derivative is also known as primitive or an indefinite integral.
Symbolically, this is written as 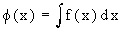 and is read as " f ( x ) is an integral of f ( x )" w.r. to x . and is read as " f ( x ) is an integral of f ( x )" w.r. to x .
Here f ( x ) is called the integrand and the process of finding the integral is called integration.
The above definition poses the following questions.
(1) Does every function poses an anti-derivative?
(2) Is an anti-derivative unique in case it exists?
(3) Is it always possible to find an anti-derivative?
The following answers are suggested :
(1) There exist a large number of functions possessing an
anti-derivative, e.g. all continuous functions. In finding
an anti-derivative, we shall always assume its existence. However
every function need not posses an anti-derivative.
(2) Let 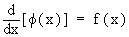 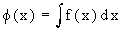 so that so that
for any constant ‘c’ 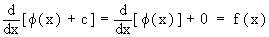
so that f ( x ) + c is also an anti-derivative of f ( x ). This accounts for the name "Indefinite Integral".
(3) In the present chapter, we shall study several methods of finding anti-derivatives. This, however, does not ensure that anti-derivative of any given function can always be obtained.
[next page]
|