|
6.7 Integration By Partial Fractions
If an algebraic fraction is expressed in terms of two or more simpler fractions, then this simple fractions are called partial fractions.
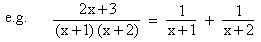
In many problems, if we resolve an algebraic fraction into partial fractions, its integration becomes much simpler.
Let the fraction to be resolved into partial fraction is 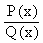 . Then there are two cases
(1) Degree of P (x) < degree of Q (x).
This algebraic fraction is known as the proper fraction.
(2) Degree of P(x) > degree of Q (x).
This type of algebraic fraction is known as an improper fraction.
Consider these cases :
(a) To each linear factor (a1x2
+ b1) of
Q (x), there will be a corresponding partial fraction in the form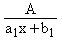 
(b) To each quadratic factor (a1x2
+ b1x
+ c1), there
will be a corresponding partial fraction in the form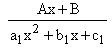 
(c) To each repeated linear factor (a1x
+ b1)n
of Q (x), there will be ‘n’ corresponding partial fractions of the
form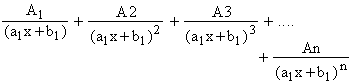 
(d) To each repeated Quadratic factor (a1x2
+ b1 +
c1
)n there will be corresponding ‘ n ’ partial fractions
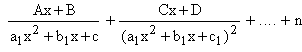as
 terms
|
