|
7.2 Definite Integral as an Area under a Curve
Observe the adjoining figure. It is clear that f (xr) Dxr is the area of the rectangle with base Dxr = xr - xr-1 and
height f (x r ).
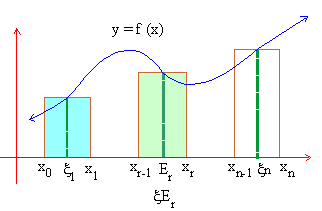
If now n ® • , in such a way that the largest of all the sub intervals, Dx1, Dx2, .......Dxn tends to zero, then we should expect that Sn would approximate to the area say A, bounded by the curve y = f (x), the x - axis and the ordinates x = a and x = b.
That is lim Sn = A, provided the limit exists .
n ® •
Example 1 Evaluate the Riemann Sum for f(x) = x2 on [1, 4] using 6 sub intervals of equal length.
Solution : Since the sub intervals are to be of equal lengths, you find that
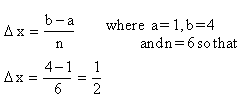
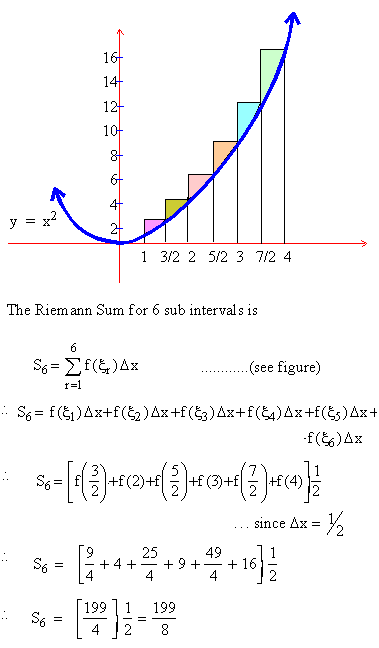
|