|
7.4 Fundamental Theorem of Integral Calculus
We have studied the definite integral 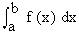 as the limit of a sum. Now we will see definite integral as the limit of a sum. Now we will see definite integral 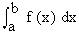 as an anti derivative. The evaluation of the definite integral as the "Limit of a sum" is a cumbersome process. (see example 2). Moreover it is not always necessary or practicable to evaluate a definite integral "ab - initio" as the "limit of a sum". For it is possible to prove that as an anti derivative. The evaluation of the definite integral as the "Limit of a sum" is a cumbersome process. (see example 2). Moreover it is not always necessary or practicable to evaluate a definite integral "ab - initio" as the "limit of a sum". For it is possible to prove that 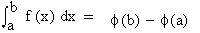 provided there exists a function such that provided there exists a function such that 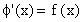 . This is given in the fundamental theorem of integral calculus as - . This is given in the fundamental theorem of integral calculus as -
If 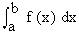 regarded as the limit of a sum exists and there exists a function regarded as the limit of a sum exists and there exists a function 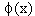 such that such that 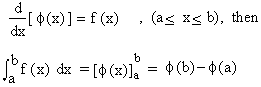
The proof of this theorem is beyond the scope of this book.
Note that in evaluating 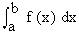 , we need not add ‘c’ to the primitive , we need not add ‘c’ to the primitive 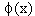 of f(x). This is evident from the fact that if we add ’c’. It is automatically eliminated. of f(x). This is evident from the fact that if we add ’c’. It is automatically eliminated.
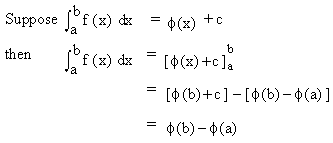
This justifies the uniqueness and the adjective "definite" for this type of integral.
Now there is a significant relationship between the continuity and differentiation. This fact leads us to say that if a function
f (x) is continuous on [a, b] then the definite integral of f (x) on [a, b] exists. Otherwise it may or may not be integrable on [a, b]. In other words, continuity guarantees the existence of the definite integral but its converse is not necessarily true.
|