4.5 Triangle
Just as the area of parallelogram was derived from the area of rectangle, the area of a triangle can be derived from the area of a parallelogram. Consider the triangle PQR (figure 4.4). If a line is drawn through P parallel to RQ and another line is drawn through Q parallel to PR they will intersect at O. POQR is a parallelogram with PQ as its diagonal.
Figure 4.4
Recall that the diagonal of a parallelogram divides the parallelogram into two congruent triangles.
\
Area of parallelogram POQR = 2 ´
Area D PQR or
Area D PQR
= 
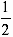Area of parallelogram POQR.
Area of parallelogram POQR = bh where h is the altitude on the base with length h.
\
Area D PQR =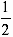
bh
Area of a triangle is half the product of one base and
the corresponding altitude.
The perimeter of the triangle is simply the sum of all its sides.
P = ( a + b + c ) in figure 4.4.
[next page]
|
