|
4.7 Circles
Perimeter of a circle is the circumference which is given by the formula.
Perimeter of a circle = 2 p
r where r is the radius, p
= 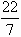 and has been discovered by ancient Greeks, by actually dividing
the circumference of a circle by its diameter .
and has been discovered by ancient Greeks, by actually dividing
the circumference of a circle by its diameter .
Area of a circle = p
r2 where ' r ' is the radius of the circle.
Example 1
If the area of a square is 16 sqft. , find the length of each side .
Solution:
Area of a square = (length of one side)2
\ length of one side = 4 ft
Example 2
If the perimeter of a square = 24 inches , What is its area ?
Solution:
If perimeter 24 inches, length of each side = 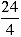 = 6 inches. = 6 inches.
\ Area = (6 inches)2
= 36 square inches.
Example 3
The perimeter of a rectangle is 36 cm, find its area if the length of one side is 12 cm.
Solution:
Area = 72 cm2
Length of the rectangle = 12 and breadth = y
\ 2 ´ 12 + 2 y = 36
24 + 2y = 36
or 2y = 12
\ y = 6 cm
Area = xy = 72 cm2
Example 4
The length of a rectangle is 10 cm and its perimeter is 30 cm. Find the area of this rectangle.
Solution:
Perimeter = 30 cm , length = 10 cm, breadth = y
2 ´ 10 + 2xy = 30
20 + 2y = 30
2y = 10
i.e. y = 5
\ area = 10 ´ 5
= 50
[next page]
|