CHAPTER 6 : THEOREM OF PYTHAGORAS AND THE RIGHT TRIANGLE
6.1 The Right Triangle
Figure 6.1
D ABC is a right triangle, hence m Ð ABC = 900. Therefore m Ð A and m Ð C are complementary ( figure 6.1). Now seg.BD is a perpendicular onto seg.AC (figure 6.2).
Figure 6.2
Seg.BD divides D ABC into two right triangles D BDC and D ADB ( figure 6.2). It can be easily proven that these two triangles are similar to the parent D ABC and therefore similar to each other.
Proof :
Consider D ABC and D BDC
Ð ABC @ Ð BDC right angles and
Ð BCA @ Ð DCB same angle
\ by AA test D ABC ~ D BDC ® (1)
Similarly consider D ABC and D ADB.
Ð ABC @ Ð ADB right angle
Ð CAB @ Ð DAB same angle
\ by AA test D ABC ~ D ADB ® (2)
from (1) and (2)
D ABC ~ D ADB ~ D BDC.
Since D ABC ~ D BDC
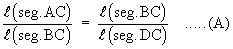
and D ABC ~ D ADB
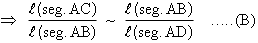
In (A) l (BC) is repeated and in (B) l (seg.AB) is repeated at the means. This is referred to as the geometric mean.
The two proportions (A) and (B) obtained by the similarity of DADB and DBDC with the original triangle are stated as a theorem as follows:
If an altitude seg.BD is drawn to the hypotenuse seg.AC of a right triangle D ABC then each leg , i.e. seg.AB and seg.BC is the geometric mean between the hypotenuse and seg.DA and seg.DC respectively ( refer figure 6.2).
The similarity of D BDC and D ADB gives the proportion.
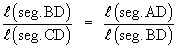
i.e. seg.BD is the geometric mean between seg.AD and seg.CD. The altitude drawn on the hypotenuse is the geometric mean between the two segments the hypotenuse is cut into.
Example 1
Find the geometric mean between :
a) 2 and 18
b) 4 and 16
c) 9 and 25
Solution :
a) 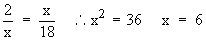
b) 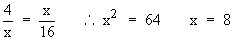
c) 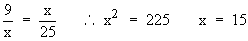
Example 2
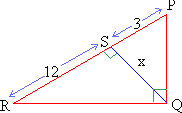 Find x. Find x.
Solution :
The square of the altitude to the hypotenuse is equal to the product of the segments cut on the hypotenuse.
\ x2 = 12 ´ 3
x2 = 36
x = 6.
Example 3
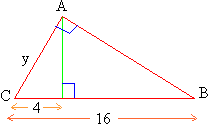 Find y. Find y.
Solution :
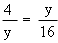
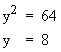
|