6.2 The Theorem of Pythagoras
Figure 6.3
D ABC is a right triangle.
l (AB) = c
l (BC) = a
l (CA) = b
CD is perpendicular to AB such that
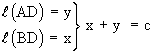
D ABC ~ D CBD
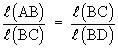
or l (BC)2 = l (AB) ´ l (CD)
a2 = c ´ x = cx® (1)
D ABC ~ D ACD
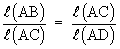
or l (AC)2 = l (AB) ´ l (AD)
b2 = c ´ y = cy ® (2)
Therefore, from (1) and (2)
a2 + b2 = cx + cy
= c ( x + y )
= c ´ c
= c2
a2 + b2 = c2
The square of the hypotenuse is equal to the sum of the squares of the legs.
Converse of Pythagoras Theorem : In a triangle if the square of the longest side is equal to the sum of the squares of the remaining two sides then the longest side is the hypotenuse and the angle opposite to it, is a right angle.
Figure 6.4
Given that in D ABC l (AC)2 = l (AB)2 + l (BC)2
To prove that D ABC is a right triangle or that
m Ð ABC = 900.
Construct a D PQR such that
l (QR) = l (BC) , l (PQ) = l (AB) & Ð PQR = 900.
In D PQR l (PR)2 = l (PQ) 2 + l (QR)2
= l (AB)2 + l (BC)2
But l (AB)2 + l (BC)2 = l (AC)2
\ l (PR)2 = l (AC)2
or that l (PR) = l (AC) ® (1)
In D ABC and D PQR
l (AB) = l (PQ) construction
l (BC) = l (QR)construction
l (AC) = l (PR) from (1)
\ D ABC @ D PQR by S S S.
\ M Ð B = M Ð Q
Since m Ð Q = 900 Ð B is a right angle and D ABC is a right triangle. Therefore if the square of the length of the longest side is equal to the sum of the squares of the other two sides the triangles is a right triangle.
|