|
8.4 Moving Fluids and Bernoulli's Equation
The motion or flow of a fluid is a complex phenomenon, which in principle can be analyzed in terms of Newtonian Mechanics, as applied to a system of particles.
Two types of flow of fluids can be characterized. They are the streamlined flow and the turbulent flow.
The flow of water in naturally occurring streams is an example of steady-streamlined flow whereas the flow of water in rapids or waterfalls is the turbulent flow.
The mechanics of fluid in the turbulent flow is beyond the scope of this book; only some aspects of the steady-streamlined flow based on the principles of conservation of mass and energy will be discussed here.
The steady-stream lined flow is characterized by stream lines and tubes of stream lines. When a non-viscous fluid flows through a certain region of space such that at a given point the velocity of all fluid particles that flow past that point is same at all times (though at different points the velocity of fluid may be different but again it will be independent of time), then such a flow is called the steady - stream lined flow. The line (curve) connecting such points is called a stream line. Stream lines have the following properties: i) Only one stream line can pass through any point. ii) A tangent at any point to the stream line represents the path of motion of a fluid particle passing through that point. 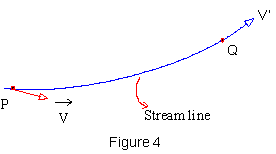
The diagram above represents a stream line. Any particle at P will have the same velocity V and will follow the same path from P to Q. Also particles that arrive at Q will have same velocity V at all times.
Tube of Flow Consider any area of Cross-section A in a fluid in a steady flow. Consider the stream lines of flow from each point on the boundary of cross-section, these stream lines enclose a tube; such a tube is called a tube of flow. The properties of tubes of flow are: i) Fluid in different tubes cannot mix with each other. ii) The same fluid particles will keep on moving through a given tube of flow. Equation of Continuity The conservation of the mass of fluid in a tube of flow, immediately results into the equation of continuity. 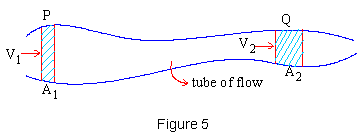
Consider the steady - Stream lined flow of a non viscous fluid; consider a tube of flow of such a fluid in motion as shown. Let P and Q be two points and let A1 and A2 be areas of cross-sections of the tube of flow normal to the velocities v1 and v2 respectively at P and Q. |
8.1 Hydrostatic pressure in a fluid Follow @Pinkmonkey_com  |
