10. Let the two numbers be a and b.

    a + b = 2 (a - b)
    a + b = 2a - 2b

              3b = a
    but       b= 10
               a = 30

    Ans : E

11. The given expression is
    

    Ans : C

12. n (A È B) = n(A) + n(B) - n(A Ç B)
    But u = n (A È B) + n (A È B)’
    n ( A È B) = 42 + 45 - 22
    n (A È B) = 65
    85 = 65 + n (A È B)’
    n (A È B)’ = 20

    Ans : B

13. 

    Since the letters represent consecutive integers, moving backwards from f to b one gets 4 units.
    \ f - b = 6 - 2 = 4

    Ans : B

14. Since the letters represent consecutive integers, the sum c + d + g = 3c + 5

    \ c + d + g = c + c + 1 + c + 4
    = 3c + 5

    Ans : A

15. 
    Since the letters represent consecutive integers, consider
    b = a + 1, c = a + 2, and d = c + 1

    To find d² - b²

    Substituting the values of d as (c + 1) and b as (a + 1)

    (c + 1)² - (a + 1)² = c² + 2c + 1 - a² - 2a - 1

    = c² - a² + 2 ( c - a)

    = 24 + 2 ( c - a) [Since c² - a² = 24]

    But c = a + 2

    \ d² - b² = 28

    Ans : E

16. 

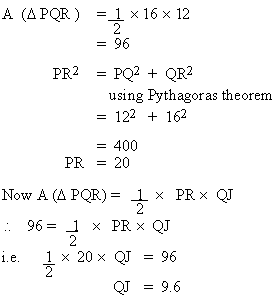
    Ans : C

    [next page]

Index