|
7.5 Polar Co-ordinates
We know how to represent points and curves in Cartesian coordinates. Another system for
such representation is the Polar System. In this system, the position of a point P on a plane is known, if we are given
(i) Its distance 'r' from a fixed point O
(ii) The inclination q of OP to OA, a fixed line through O.
Here the fixed point is called the pole, or origin. The fixed line OA (which is usually situated
horizontally) is called the polar axis. 'r' is called the 'radius vector' of P and 'q' is called the 'vectorial angle'. If the angle is measured counter clock-wise sense, it is positive or if it is measured in clockwise
sense, then it is negative.
Note that point P if on the terminal side of angle q then r is positive. If P is on the opposite side of the pole then r is negative.
The two 'r' and 'q', are now called the polar coordinates of P and written as an ordered pair
(r,q).
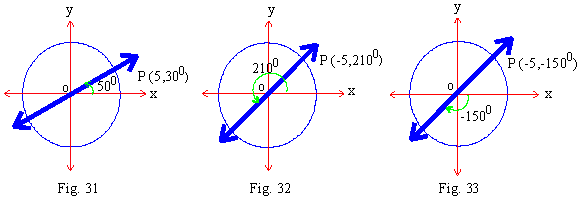
The location of a point can be named in many different pairs of polar coordinates. Following
figures illustrate three different sets of Polar Coordinates of point P (5,
300).
Click here to enlarge
For changing from Cartesian to Polar
coordinates, or vice versa, we take origin as pole. The x-axis as the initial line or the polar axis.
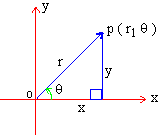
Then x = r cos q, y = r sin q ........(i)
are the formulas, for converting from Cartesian to Polar
from (i) x2 + y2 = r2 and q = tan-1 (y/x) .....(ii)
We use (ii) for the conversion from Polar to Cartesian Co-ordinates.
|