|
CHAPTER 8 : COMPLEX NUMBERS
8.1 Geometry of Complex Numbers
The set of real numbers seems to fulfil the need
to algebra. But at times in algebra too, a state is reached when
a set of real numbers falls short. For example, it is impossible
to solve
the quadratic equation x2+ 16 = 0 in terms of real roots.
For, x2= - 16 leads to x =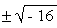 
, where the square root of -16 can not be extracted in terms of
any real number. In other words this means, there is no real number
whose square is - 16. At the most we simplify 
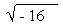
as,
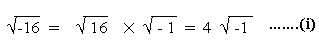
At this stage we introduce a new kind of number
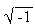, which is different from the real numbers and hence called an "imaginary
number", usually denoted by 'i'. It is customary to designate
'i' by 'j' in most of the work in electrical engineering . This
number permits the
solution of the above equation and those similar
to it. This number i =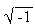
such that i2 = -1.
The symbol 'i' now enables us to write (i) as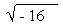
= 4
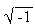= 4i. The credit of introducing 'i' goes to an eminent French mathematician
Euler (1707 - 1783).
Power of 'i' : More often, while
effecting easy operations with complex number, we come across with
various powers of 'i'. The following illustrations would serve a
guidance in such cases
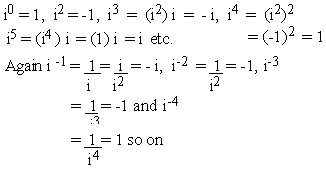
[Thus in = ± 1 or ± i ]
This requires the knowledge of indices and a bit
careful working.
[next page]
|
