EXAMPLE 5 Transform the following into rectangular form:
(i) r = -3 (ii) r = a cos q (iii) r = b sin q (iv) q = a (v) b cosec q (vi) r = a sec q (vii) r = a (1 + cos q) (viii) r = a (1 + sin q) (ix) r =

Solution :

1. r = -3,   squaring   both   sides   we  get r² = 9      then r²(cos² q + sin² q) = 9

   \ r² cos² q + r² sin² q = 9

   \ (r cos q)2 + (r sin q)2 = 9

   put r cos q = x and r sin q = y we get x² + y² = 9 which is a circle of radius '3' and centre (0, 0).

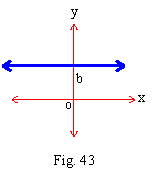
2. r = a cos q

   \ r² = ra cos q

   \   r²(cos² q + sin2 q) = a (r cos q)

   \   r² cos² q + r² sin² q = a (r cos q)

   \   (r cos q)² + (r sin q)² = a (r cos q)

   \   (x)² + (y)² = a (x) ... x = r cos q and y = r sin q

   \ x² + y² - ax = 0

   

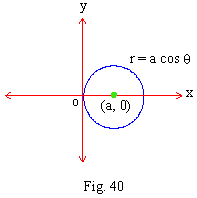
3. r = b sin q \ r² = b r sin q

   \ x² + y² = b (y)

   since r² = x² + y² and r sin q = y

   \ x² + y² - by = 0

   

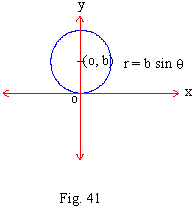
4. q = a which is a straight line through origin.

   

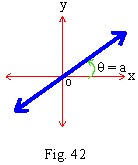
5. r = b cosec q

   \ r =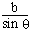

   \ r sin q = b

   \ y = b which is a straight line parallel to x - axis at a distance 'b' unit from the origin.

   
   [next page]

Index

7.1 Scalers & Vectors
7.2 Algebra of Vectors
7.3 Representation of a vector in a plane
7.4 Dotor Scalar product
7.5 Polar Co-ordinates
Supplementary Problems

Chapter 8