-
Many valued function: To each value of x, suppose
there are more than one value of y, then y is called a multiple
valued or many valued function.
e.g. y2 = 4ax ; x2
+ y2 = a2 ; y (y-2) (y +2) = x2
-
The mapping of function f: x ®
y is said to be Many-One if two or more different elements
in x have same f-image in y.
-
The mapping or function f is said to be One-One
if different element in x have different f-images in y, i.e.
x1 ¹ x2 Þ
f (x1) ¹ f ( x2)
or f (x1) = f (x2) Þ
x1 = x2.
One-One mappings are also called injection
or injective mappings.
-
The mapping 'f ' is said to be 'into' if there
exists at least one element in y which is not the f-image of
any element in x. Note that in this case range of ’f’ is the
proper subset of y.
-
The mapping 'f ' is said to be 'onto' if every
element in y is the f-image of at least one element in x. In
this case, the range of 'f ' is equal to y. 'Onto' mapping is
also called surjection or Surjective mappings.
One-One and onto mappings are called bijection
or bijective mappings.
If the domain and codomain of a function f
are both the same, then f is called an operator or
transformation on x.
-
Odd and Even functions : If f(-x) = f(x), f(x)
is called an even function.
e.g. f(x) = ax4+ bx2
+ c, f (x) = cos x etc.
If f (-x) = -f (x), f (x) is called an
odd function.
e.g. f(x) = ax3 + bx , f(x) = tan x etc.
Note that any function can be expressed as the sum of an
even and odd function.
viz. 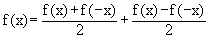
-
Explicit and Implicit functions : A function
is said to be explicit when expressed directly in terms of the
independent variable or variables. e.g. y = e-x.
xn , y = r sin q etc.
But if the function cannot be expressed
directly in terms of the independent variable (or variables),
the function is said to be implicit. e.g. x2y2
+ 4xy + 3y + 5x + 6 = 0. Here y is implicit function of 'x'.