|
4.3 Derivability and Continuity of A Function At A Point
THEOREM: If a function ‘f ’ is derivable at x, then ‘f ’
is continuous at x.
PROOF: We are given that ‘f’ is derivable at x
\ f ’ (x) = 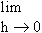
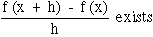
REMARK: The converse of this theorem i.e. " If ‘f ’
is continuous at ‘x’ , then ‘f’ is derivable at ‘x’ " is not
true. This can be seen from the following examples.
Example 3
Shows that the function f defined by f(x) = |x| is continuous but
not derivable at x = 0.
We have f (0) = 0 and 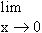 |x| = 0. Hence |x| = 0. Hence 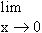 f (x) = f (0) and ‘f ’ is continuous at x = 0. f (x) = f (0) and ‘f ’ is continuous at x = 0.
From Example 1 we have already proved that ‘f ’ is not derivable at x = 0
Example 4
If f (x) = x sin 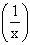 , x ¹ 0 and f (0) = 0, show that ‘f ’
is continuous but not derivable at x = 0.
, x ¹ 0 and f (0) = 0, show that ‘f ’
is continuous but not derivable at x = 0.
We have f (0) = 0 and 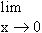 x sin
x sin 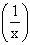 = (a finite limit) ´
0 = 0 since sin
= (a finite limit) ´
0 = 0 since sin 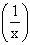 always lies between -1 and 1 for any value of x.
always lies between -1 and 1 for any value of x.
Therefore -|x| £
x sin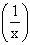 £
|x| £
|x|
But 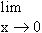 |x| = 0 and
|x| = 0 and 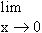 - |x| = 0 Þ
- |x| = 0 Þ 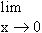 x sin
x sin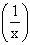 = 0
= 0
Now f "(0) = 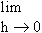 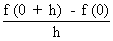
= 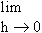 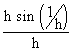 , for the given function. , for the given function.
\ f ’ (0) = 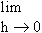 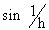 which does not exist, Hence ‘f ’ is not derivable at x = 0
which does not exist, Hence ‘f ’ is not derivable at x = 0
|