1) If u and v are differentiable functions of x, then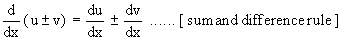

In general the derivative of the sum ( or difference ) of two or more functions w.r. to x is the sum ( or difference ) of their derivatives w.r. to x.

2) If u and v are differentiable functions of x, then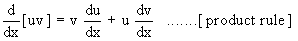

Corollary:    If k is constant and f (x) is a differentiable function of x, then

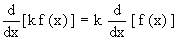
Corollary: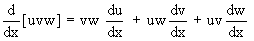   

3) If u and v are differentiable functions of x, then

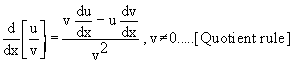
Corollary :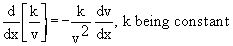   

Proofs : 1) Let y = u ± v

Let D y, D u and D v be changes in y, u and v respectively corresponding to a change D x in x.

Then y + Dy = ( u + Du) ± ( v + Dv )

subtracting, we get, Dy = Du ± Dv

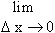
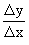
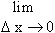
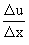
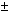
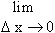
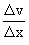
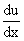
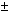
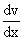
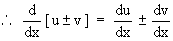
2) Let y = u.v

Let Dy, Du, Dv be changes in y, u and v respectively corresponding to a small change Dx in x.

Index

4. 1 Derivability At A Point
4. 2 Derivability In An Interval
4. 3 Derivability And Continuity Of A Function At A Point
4. 4 Some Counter Examples
4. 5 Interpretation Of Derivatives
4. 6 Theorems On Derivatives (differentiation Rules)
4. 7 Derivatives Of Standard Functions
4. 8 Derivative Of A Composite Function
4. 9 Differentiation Of Implicit Functions
4.10 Derivative Of An Inverse Function
4.11 Derivatives Of Inverse Trigonometric Functions
4.12 Derivatives Of Exponential & Logarithmic Functions
4.13 Logarithmic Differentiation
4.14 Derivatives Of Functions In Parametric Form
4.15 Higher order Derivatives

Chapter 5

Follow @Pinkmonkey_com