Then y + Dy = (u + Dx) (v + Dx) = uv + v Du + u Dv + Du . Dv.

Subtracting we get, Dy = v du + u dv + Du . Dv

\

\

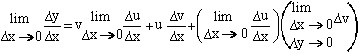
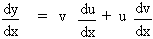
i.e.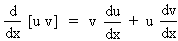

(3) Let y = u / v. Let Dy , Du and Dv be changes in y, u and v respectively in y, u and v respectively corresponding to a small change Dx in x.

Then     y + Dy =

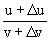
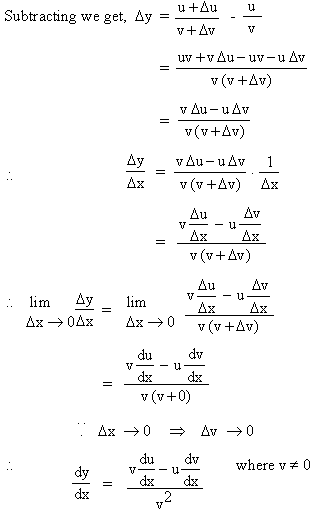
Index

4. 1 Derivability At A Point
4. 2 Derivability In An Interval
4. 3 Derivability And Continuity Of A Function At A Point
4. 4 Some Counter Examples
4. 5 Interpretation Of Derivatives
4. 6 Theorems On Derivatives (differentiation Rules)
4. 7 Derivatives Of Standard Functions
4. 8 Derivative Of A Composite Function
4. 9 Differentiation Of Implicit Functions
4.10 Derivative Of An Inverse Function
4.11 Derivatives Of Inverse Trigonometric Functions
4.12 Derivatives Of Exponential & Logarithmic Functions
4.13 Logarithmic Differentiation
4.14 Derivatives Of Functions In Parametric Form
4.15 Higher order Derivatives

Chapter 5

Follow @Pinkmonkey_com