(1) The condition that f ' (x) i.e.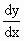 
= 0 at x = c, for f (x) should be maximum or minimum is necessary but it is not sufficient
Hence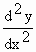 
at x = 0 is neither negative nor positive
hence at x = c is neither a maximum nor a minimum.
(2) The maxima and minima of f(x) are also known as 'turning
values' of f(x) since
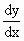changes its sign from positive to negative or from negative to positive.
They are also known as "extrema or extreme values."
(3) The values of the function for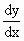
= 0 are known as critical values or stationary values
since f (x) is neither increasing nor decreasing at these values
(points). It is a value or point at which the gradient
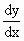is zero.
Note that a stationary point is not necessarily a turning point.
It is clear from the above example given in (1). At (0, 0)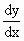
= 0 and the x - axis is the tangent there. However, (0, 0) is not
a turning point because f (x) continues to increase when passing
through it. The origin is stationary since the curve y = f (x) is
momentarily stationary there.
= 6x then at x = 0,